平衡状态下，PN结是没有电流的。但外加电压后，这种平衡状态被打破，使得电流产生。外加电压分为两种情况，N区接正电压，PN结处于反偏状态，P区接正电压，PN结处于正偏状态。正偏与反偏情况下的PN结的特性是差很多的。我们知道，半导体的特性主要是载流子分布、输运、电场电势等引起的，我们分析也是从这些角度入手。首先来看反偏状态。

反偏时的载流子输运

当N区接正电压后，会排斥N区的空穴，即将N区的空穴推向P区。同理，P区的电子会被排斥到N区。达到稳定状态后，这个电子流和空穴流就形成了电流。但我们知道，空穴在N区中是少子，电子在P区中是少子，其浓度很低。因此，这个电流会很小。这就是我们常说的二极管反偏时电流很小的原因。

由于电流很小，落在耗尽区两端的电压可以忽略不计，相当于外加的电压全部降落在了耗尽区中。因此，耗尽区承受的电压，也就是势垒，从原来的$q\phi_{bi}$变为了$q\phi_{bi}+qV_r$，增加了$qV_r$。

我们也可以换个角度来理解这个问题。反偏时，外加电压对应的电场方向与内建电场方向一致，都是N->P，电场影响的是漂移运动，阻碍的是扩散运动。因此，漂移运动增加，扩散运动减弱。扩散运动的阻碍增加反映在能带图中就是那堵阻碍扩散运动的墙变高了，也就是势垒变高。同时，两端的费米能级也不再统一，而是发生了分裂，很容易得到两边的费米能级差了$qV_r$。能带图如下：

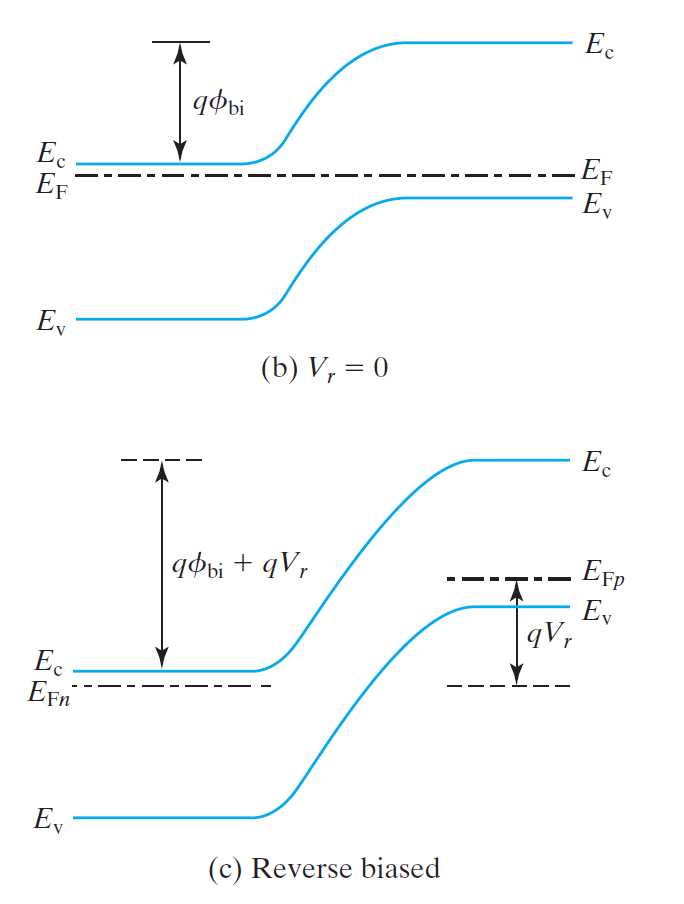
从上一篇文章的推导中，我们可以很容易得到反偏状态下的耗尽区宽度，将式子中的$\phi_{bi}$变为了$\phi_{bi}+V_r$，即：

$$
W_{\text {dep }}=\sqrt{\frac{2 \varepsilon_s\left(\phi_{\mathrm{bi}}+V_r\right)}{q N}}=\sqrt{\frac{2 \varepsilon_s \times \text { potential barrier }}{q N}}
$$

这是一个很重要的式子。我们可以发现，反偏时势垒高度增加，耗尽区宽度也随之增加。我们可以用一句话更形象的描述这个现象，那就是耗尽区需要扩展去抵消外界电压带来的压降。这句话给人一种“外界给我的压力增加了，我需要变得更强大才能去承受它”的感觉，可以帮助我们很好的理解这个现象。

我们再来聊一下这个电流。由于耗尽区边界处的少子被推走，从而形成浓度梯度，远离耗尽区出的少子会补充过来，形成扩散电流。但是由于少子本身浓度很低，故浓度梯度很低，故扩散电流很小。N区的空穴来到P区后，也会进行扩散，但这部分空穴相比于P区本身的空穴是很小很小的，可以忽略不计，因此，在P区，空穴准费米能级是几乎不变的。耗尽区内近似没有载流子，因此，耗尽区内的$E_{Fn}$与N区的$E_{Fn}$是相等的，$E_{Fp}$与P区的$E_{Fp}$是相等的。在N区耗尽区边界处，外加反偏电压前，$E_{Fp}$与$E_{Fn}$是相等的，外加电压后，$E_{Fp}$升高了$qV_r$，因此，我们可以得到，空穴浓度减小了$exp(\frac{qV_r}{k_0T})$倍，即N区耗尽区边界处的空穴浓度为$p_{n0}/exp(\frac{qV_r}{k_0T})$。本身空穴浓度$p_{n0}$就很小，处于一个指数项，就更小了，因此，可以近似认为反偏时耗尽区边界处的少子浓度为0。这种现象就好像是少数载流子被不断地抽取，因此，反偏时载流子的特点可以总结成七个字：少数载流子抽取。

C-V特性

耗尽区宽度的变化对应着耗尽区电容的变化。

$$
C_{\mathrm{dep}}=A \frac{\varepsilon_s}{W_{\mathrm{dep}}}
$$

将耗尽区公式代入，并进行变换一下，得到：

$$
\frac{1}{C_{\mathrm{dep}}^2}=\frac{W_{\mathrm{dep}}^2}{A^2 \varepsilon_s^2}=\frac{2\left(\phi_{\mathrm{bi}}+V_r\right)}{q N \varepsilon_s A^2}
$$

从这个式子中可以发现，$\frac{1}{C_{\mathrm{dep}}^2}$与外加电压$V_r$成线性关系。这是一个很有用的曲线，在半导体测试中，我们常常需要测试杂质分布，通过外加不同的电压，得到不同的耗尽区宽度，绘制出C-V特性曲线，就可以测出不同位置处的掺杂浓度。

击穿特性

前文中提到，反偏电流是很小的，但是实验发现，当反偏电压增加到一定程度后，反向电流密度会突然迅速增加，这就是PN结击穿。这个可以形象的描述为，耗尽区通过扩展来抵挡外界电压，而当外界电压过强，耗尽区就无法承受了，于是就击穿了。

PN结击穿主要有三种，分别是雪崩击穿、隧道击穿（齐纳击穿）、热电击穿。这里主要介绍前两种，这两种也是最重要的两种击穿。

雪崩击穿

反偏时，半导体内部的电场会增强。当反偏电压很大时，内建电场很强，从N区漂移到P区的空穴和P区漂移到N区的电子在强电场作用下，会获得很大的动能。我们知道，价电子通过共价键被束缚在晶格中，当价电子拥有足够的能量时，将会脱离晶格称为自由电子。这些具有很大动能的电子和空穴在穿越耗尽区的时候，肯定会与晶格中的原子发生碰撞，高能量使得价电子脱离了共价键的束缚，成为了导电电子，同时产生一个空穴。从能带角度看，这是高能量的电子和空穴把一部分能量传递给价带中的电子，使其激发到导带，产生了一个电子-空穴对。然后激发出的电子和空穴将会在电场作用下加速，获得高能量，再激发出其他的电子-空穴对。于是就产生了一种现象，一个电子碰撞出来了一个电子和一个空穴，于是变成了三个载流子，然后在强电场作用下继续碰撞，每一个又能碰撞出三个载流子，如此继续下去，载流子大量增加，这就是载流子的倍增效应。倍增效应是一个很重要的概念，而不仅仅用于雪崩击穿中，它的本质是载流子能量的传递，只要有高能量，就可能会发生倍增效应，高电场只是产生倍增效应的一种方式，比如光电倍增管就是利用了倍增效用。

当倍增效应发生后，耗尽区将不再耗尽，而是有着大量的载流子，反向电流迅速增大。这就是雪崩击穿。

那雪崩击穿的影响因素有什么呢？我们可以从雪崩击穿的原理来看：

首先是电场要强，即反偏电压很高，这是毋庸置疑的

雪崩击穿电压一般都要很大，远大于$\phi_{\mathrm{bi}}$，因此势垒高度近似为反偏电压。假如达到倍增效应时的临界电场为$\mathscr{E}_{crit}$，我们根据耗尽区宽度的公式和$V=Ed$求出雪崩击穿电压：

$$
V_{\mathrm{B}}=\frac{\varepsilon_s{\mathscr{E}_{\text {crit }}}{ }^2}{2 q N}
$$

因此，我们可以发现，如果想要增大雪崩击穿电压，需要降低掺杂浓度。

最后，我们来探讨一下雪崩击穿和温度的关系。雪崩击穿从机理上来说，和温度并无太大关系。但我们知道，载流子在半导体中运动，并不是直线运动、畅通无阻的，是不断的进行散射的。散射不利于载流子速度的积累。因此，温度升高后，散射增强，雪崩击穿更不易发生，雪崩击穿电压增大。

结论：降低掺杂浓度、升高温度可以提高雪崩击穿电压。

想要提高雪崩击穿电压还可以从材料入手，比如说，禁带宽度越大，价电子越不容易跃迁到导带，提高了雪崩击穿电压。

隧道击穿（齐纳击穿）

隧道效应是当器件尺寸降低后，不可忽视的一个效应。隧道击穿的核心是隧道效应，由隧道效应，使大量电子从价带穿过禁带而进入到导带所引起的一种击穿效应。

如下图所示，图中P区价带中的电子如果想要从P区到N区，需要先跃迁到导带上，然后再发射到N区。我们知道，P区中，跃迁到导带中的电子很少，电子是少子，所以电流很小。如果电子未得到能量，在经典力学中，这个电子是不可能到N区的。但是，从量子力学的角度，将会产生不一样的现象。

量子力学中，有一个能量-时间不确定性原理。简单来说，假如一个粒子的能量为$E$，根据不确定性原理，它可以在$\Delta t$的时间内借得$\Delta E$的能量，那么这个粒子的能量将短暂的变为$E+\Delta E$，即能量是不确定的。但是，这个粒子并不能永久性的拥有这个借来的能量，必须要在$\Delta t \approx \hbar / 2 \Delta E$的时间内还回去。根据这个式子，可以知道，借的能量越多，拥有这个能量的时间就越少。

再考虑上面这个问题，如果这个电子想要到N区。假设它借到了足够的能量，然后如果它能在$\Delta t$时间内运动到N区中，然后还回能量$\Delta E$，那么它就成功的到了N区。在我们的视角上看，它就像是从P区直接穿透到了N区，这就是隧穿效应。如下图所示：

根据隧穿效应的原理，我们可以知道，在上面的能带图中，电子要隧穿到N区的导带中，当电子借到能量并运动到N区后，需要将借来的能量还回去，相当于能量回到了最初的水平，此时如果N区导带的能量比P区价带能量高，那么电子将无法成功的落到N区导带中。此时就隧穿失败了，会被反弹回去。因此，在PN结中，发生隧道击穿时，能带上N区导带要在P区价带的下面！！！即PN结处于一个大的反偏电压下，因此，当反偏电压很大时，PN结可能发生隧道击穿。

接下来我们来看隧道击穿的影响因素。

如果这个耗尽区很厚，那么粒子拥有借来能量的时间就很短，粒子穿透过去的概率就很低，大多数粒子都会被反弹回去。因此，需要耗尽区宽度尽可能低，这就要求高掺杂浓度。

接下里看温度的影响，首先是温度升高，禁带宽度往往会减小，因此电子发生隧穿需要借的能量减小，更容易隧穿。下面是我的理解，温度升高提高了整个系统的能量，电子自身能量增加同时也能更容易借到能量，因此隧穿概率增大。因此，温度升高，隧穿概率增加，隧道击穿电压减小，具有负温度系数。

隧穿还可以用德布罗意波的角度来解释，粒子具有波动性。隧穿后的电子也并不是毫无损失，其再次越过势垒的可能性相比之前会降低，只不过是能量未变。由于我也不是很懂，这里就不多说了。隧穿效应的应用是十分广泛的，有研究表明隧穿电流与介质层厚度是指数关系，因此，势垒厚度改变会引起电流指数级的变化，因此，可以利用电流来观测介质层的结构。这个就是扫描隧道显微镜的原理。

因此，一般来说，在低浓度情况下，雪崩击穿是主要的，在高浓度时，隧道击穿是主要的。