有限差分法
差分格式
首先,我们需要对空间坐标进行离散化,也成为网格化(mesh)。网格化是器件仿真中十分重要的内容,合理的网格设置不仅可以帮助我们得到准确的结果,也能帮助我们减少模型的计算量,提高工作效率。在 TCAD 软件中,有许多的网格设置方法,但总归来说,都是通过一定的方式(比如说给定函数)对连续坐标进行离散化,把握好这个关键就很好理解 TCAD 中的一些网格设置。
将数据离散化之后,我们就可以将微分形式转换为差分形式。这个方法有很多,最简单的便是 Euler 法,还有 Runge-Kutta 法等,但这些方法的核心依旧是 Euler 法,感兴趣的可以去学一学微分方程数值解法。在这里,我们按下图所示的方式对数据离散化:

根据微分的定义,我们可以将 $x_k$ 处的值近似表示为:
$$
\frac{df}{dx_k}=\frac{f(x_{k+1})-f(x_k)}{d_k}
$$
这个便是其中的一种差分格式,叫做向前差分。在这里,我们考虑利用如下的差分形式。如下图所示,将中点记为 M。
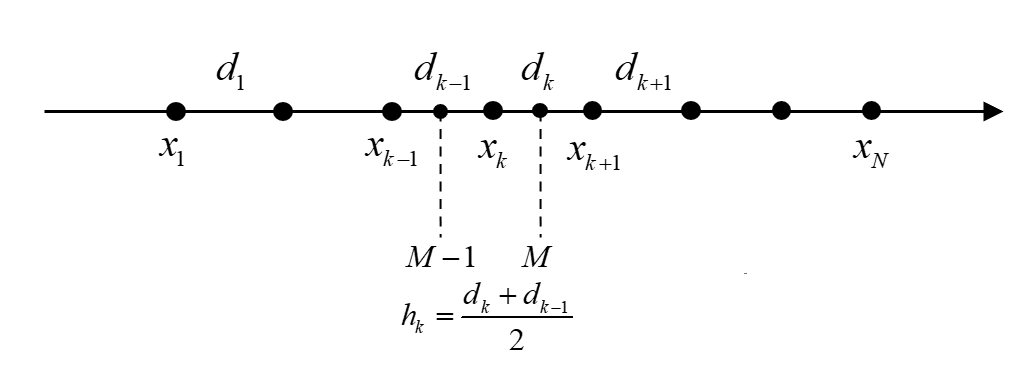
令:
$$
\frac{df}{dx_k}=\frac{f(x_{M})-f(x_{M-1})}{h_k}
$$
由此可以得到二阶导为:
$$
\frac{d^{2}f}{dx_{k}^{2}}=\frac{f'(x_{M})-f'(x_{M-1})}{h_{k}}=\frac{\frac{f(x_{k+1})-f(x_k)}{d_k}-\frac{f(x_{k})-f(x_{k-1})}{d_{k-1}}}{h_{k}}
$$
由于 M 对应的点并不是我们网格上的点,因此,我们需要把 M 转化到 k 上。我们假设在每一段上线性变化,即:
$$
f(x_{M})=\frac{f(x_{k})+f(x_{k+1})}{2}
$$
代入到上面的式子中,可以得到:
$$
\frac{df}{dx_k}=\frac{f(x_{M})-f(x_{M-1})}{h_k}=\frac{\frac{f(x_{k})+f(x_{k+1})}{2}-\frac{f(x_{k})+f(x_{k-1})}{2}}{h_k}=\frac{f(x_{k+1})-f(x_{k-1})}{d_{k}+d_{k-1}}
$$
有了上面的关系,我们就可以把微分方程转化为差分方程了,如下:
$$
\begin{aligned}
&\frac{2}{d_{k-1}+d_{k}}(\frac{\varphi_{k+1}-\varphi_{k}}{d_{k}}-\frac{\varphi_{k}-\varphi_{k-1}}{d_{k-1}})=-(N_{k}+p_{k}-n_{k}) \\
& \frac{J_{p,k+1}-J_{p,k-1}}{d_{k-1}+d_{k}}=-R_{k} \\
& \frac{J_{n,k+1}-J_{n,k-1}}{d_{k-1}+d_{k}}=R_{k} \\
& \frac{n_{k+1}-n_{k-1}}{d_{k-1}+d_{k}}=\frac{J_{n,k}}{\mu_{n}}+n_{k}\cdot \frac{\varphi_{k+1}-\varphi_{k-1}}{d_{k-1}+d_{k}} \\
& \frac{p_{k+1}-p_{k-1}}{d_{k-1}+d_{k}}=-\frac{J_{p,k}}{\mu_{p}}-p_{k}\cdot \frac{\varphi_{k+1}-\varphi_{k-1}}{d_{k-1}+d_{k}} \\
& R_{k}=\frac{n_{k}p_{k}-1}{\tau_{p}(n_{k}+1)+\tau_{n}(p_{k}+1)}
\end{aligned}
$$
显然,在这个方程中,$J,R$ 都是中间量,可以消去,最后得到关于 $\varphi,n,p$ 的方程。
第一个方程可以写成:
$$
F_{\varphi}(n_{k},p_{k},\varphi_{k-1},\varphi_{k},\varphi_{k+1})=0
$$
将有关 p 的方程联立,可以得到:
$$
F_{p}(n_{k-1},n_{k},n_{k+1},p_{k},\varphi_{k-1},\varphi_{k},\varphi_{k+1})=0
$$
将有关 n 的方程联立,可以得到:
$$
F_{n}(p_{k-1},p_{k},p_{k+1},n_{k},\varphi_{k-1},\varphi_{k},\varphi_{k+1})=0
$$
由于这些方程都是对于内部的点,而非边界点,因此方程的个数共有 $3(N-2)$,未知量个数也是 $3(N-2)$ 个,因此理论上是可以解的。
方程个数这么多,得到理论解几乎是不可能的,因此在实际中常常采用迭代法。迭代的方法有很多,常用的是牛顿迭代法。
牛顿迭代法
只有一个方程的情形
$$
f(x)=0
$$
牛顿迭代法的原理如图所示:
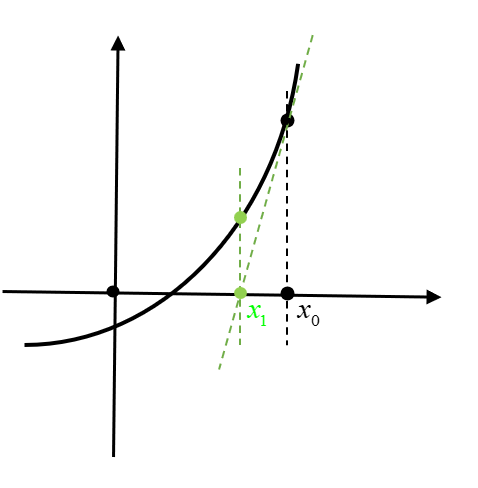
首先,我们需要给定一个初值 $x_0$,然后过这个点作切线。我们可以得到切线方程为:
$$
y=f'(x_{0})(x-x_{0})+f(x_{0})
$$
令 $y=0$,可以求得该切线与 x 轴的交点坐标。可以得到:
$$
x_{1}=x_{0}-\frac{f(x_{0})}{f'(x_{0})}
$$
从图中可以发现,该点距离最终的结果更近了一步。就这样迭代下去,便可以得到接近目标值的解。其迭代方程为:
$$
x_{k+1}=x_{k}-\frac{f(x_{k})}{f'(x_{k})}
$$
方程组情形
$$
\begin{aligned}
f_{1}(x_{1},x_{2},\cdots ,x_{n})&=0 \\
f_{2}(x_{1},x_{2},\cdots ,x_{n})&=0 \\
\vdots \\
f_{n}(x_{1},x_{2},\cdots ,x_{n})&=0
\end{aligned}
$$
首先,我们把自变量和因变量都写成向量的形式,令:
$$
\mathbf{X}=(x_{1}, x_{2},\cdots, x_{n})^T
$$
$$
\mathbf{F}=(f_{1}, f_{2}, \cdots, f_{n})^T
$$
则上述方程组可以写成:
$$
\mathbf{F(X)}=0
$$
当只有一个方程时,我们得到:
$$
x_{k+1}=x_{k}-\frac{f(x_{k})}{f'(x_{k})}
$$
我们可以对其进行推广,这是数学研究中十分常用的方法。首先,在矩阵中,除法表现为逆,故将 $f'(x_{k})$ 推广为一个矩阵的逆,记为 $\mathbf{F'(X^{k})}^{-1}$,然后我们就能够得到:
$$
\mathbf{X^{k+1}}=\mathbf{X^{k}}-\mathbf{F'(X^{k})}^{-1}\mathbf{F(X^{k})}
$$
而这个便是方程组时的牛顿迭代法的递推公式。接下来的问题就是这个 $\mathbf{F'(X^{k})}$ 是什么,要怎么求。
首先,我们知道 $\mathbf{X,F}$ 均为 $n\times 1$ 的矩阵,故 $\mathbf{F'(X^{k})}^{-1}$ 为 $n\times n$ 的矩阵,所以 $\mathbf{F'(X^{k})}$ 也为 $n\times n$ 的矩阵,这个矩阵便是雅可比矩阵(Jacobian matrix)。雅可比矩阵的形式如下:
$$
\mathbf{J} = \begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\
\vdots & \ddots & \vdots \\
\frac{\partial f_n}{\partial x_1} & \cdots & \frac{\partial f_n}{\partial x_n}
\end{bmatrix}
$$
从这个具体形式中可以看出,雅可比矩阵描述了多元函数的局部线性近似的信息。如何理解雅可比矩阵是怎么导出的呢?可以这么简单理解:
考虑一个二元方程组,即:
$$
\begin{aligned}
f_1(x_1,x_{2})=0 \\
f_{2}(x_{1},x_{2})=0
\end{aligned}
$$
仿照着一元方程的做法,考虑 $f_1(x_1,x_2)$,根据全微分的知识,我们知道这个二元函数的变化率为:
$$
df_{1}^k=\frac{\partial f_1^k}{\partial x_1}dx_{1}^k+\frac{\partial f_1^k}{\partial x_2}dx_2^k
$$
故
$$
f_{1}^{k+1}=f_{1}^{k}+df_{1}^{k}=f_{1}^{k}+\frac{\partial f_1^k}{\partial x_1}dx_{1}^k+\frac{\partial f_1^k}{\partial x_2}dx_2^k
$$
这可以看作是 $x^k$ 点处的一小段直线的表达式,我们可以将其扩展成一个直线方程:
$$
f=f_{1}^{k}+\frac{\partial f_1^k}{\partial x_1}(x_1-x_{1}^k)+\frac{\partial f_1^k}{\partial x_2}(x_2-x_{2}^k)=f_{1}^{k}+\begin{bmatrix}
\frac{\partial f_1^k}{\partial x_1}&\frac{\partial f_1^k}{\partial x_2}
\end{bmatrix}
\begin{bmatrix}
x_1-x_{1}^k\\x_2-x_{2}^k
\end{bmatrix}
$$
同样的,我们考虑 $f_2$,就可以得到另一个方程,然后将两个方程联立,写成矩阵形式,便可以得到解了,就可以发现导数矩阵就是雅可比矩阵。
牛顿迭代法的流程
综上所述,我们可以得到求解方程组的流程,如下:
- 选择初始猜测向量 $\mathbf{X^{0}}=[x_1^0,\cdots,x_n^0]$.
- 计算函数值 $\mathbf{F(X^0)}$ 和雅可比矩阵 $\mathbf{J(X^0)}$.
- 计算雅可比矩阵的逆 $\mathbf{J(X^0)}^{-1}$.
- 计算下一个近似解 $\mathbf{X^1}=\mathbf{X^{0}}-\mathbf{J(X^{0})}^{-1}\mathbf{F(X^{0})}$.
- 重复步骤 2~4,直到满足收敛条件为止。
总结
通过牛顿迭代法,我们就可以设计程序,利用计算机对上面的 $3(N-2)$ 个方程求解。