PN结的部分我主要分为了三个部分,分别为:
- 平衡状态下的PN结
- 非平衡状态下的PN结的特性,主要是正偏和反偏的特性以及两条曲线,分为下面
- 反偏特性和C-V曲线
- 正偏特性和I-V曲线
- PN结的应用拓展
在开始前,我想提一句话,那就是PN结也是在一个半导体上的,其分析方法和前面讲到的费米分布、载流子输运等用到的分析方法相同,无非就是复杂了一些而已。但只要将前面的内容套用进来,认真推导一下,就可以得出PN结中的很多结论。PN结是学好器件的基础,学好PN结后,后面的BJT、肖特基结、MOS等学起来都会轻松很多,因为它们本质上无非就是载流子的输运,导致载流子的再分布,从而有着各种各样的性质。
下面正式开始第一部分。
PN结
在前面的内容中,我们的讨论对象要么是N型半导体,要么是P型半导体。而如果把一块N型半导体和一块P型半导体结合在一起后,会发生什么呢?此时,在两个类型的半导体的交界处,就会形成PN结。
在之后的讨论中,以一种最简单的情况为例,即N型区均匀掺杂,掺杂浓度为$N_d$,P型区均匀掺杂,掺杂浓度为$N_a$,且都完全电离,在交界处,杂质浓度发生了突变,即突变结。而学过工艺的同学肯定知道,在实际工艺中,更常使用的方式是采用扩散的方法制备PN结,即利用浓度梯度,使得杂质不断往深处扩散,从而得到一个杂质分布。这样得到的PN结杂质分布是缓变的。但不论是突变结还是缓变结,工作原理都是相同的,因此在这里,以最简单的突变结为例。
由于P型区和N型区载流子浓度不同,从而发生扩散。N型区的电子浓度高,将会扩散进入P型区,我们之前强调过,施主杂质在提供电子的时候会留下正电中心,因此,电子扩散进入P型区的时候,会留下不可动的正电中心。由于原先与它保持电中性的电子跑到了P区,因此形成了一个正电荷区。同理,P区的空穴扩散进N区,留下了负电中心,形成了一个负电荷区。PN结附近的这些形成带电区的正电中心和负电中心所带的电荷称为空间电荷,它们所在的区域称为空间电荷区。
空间电荷区形成后,由于N区带正电,P区带负电,那么将会形成内建电场,其电场方向由N指向P区。我们知道,当存在电场时,载流子会发生漂移运动。由于电场方向由N指向P,那么电子将会从P区漂移到N区,空穴会从N区漂移到P区,此时电子和空穴的漂移运动方向与扩散运动方向相反,相当于阻碍了扩散运动的进行。
随着扩散运动的逐渐进行,空间电荷增加,空间电荷区扩展,内建电场增强,从而使得漂移运动增强,扩散运动的阻力增加。最终,会形成一个稳定状态,即扩散运动和漂移运动达到了平衡。

思考一个问题,此时PN结有电流吗?
答案是没有电流,这是因为达到平衡后,扩散电流和漂移电流大小相等,方向相反,互相抵消。总结一下平衡时PN结的特点:空间电荷的数量保持一定,空间电荷区保持一定的宽度,存在一定的内建电场。
能带图
当PN结达到热平衡后,那么将拥有统一的费米势。根据费米能级的含义(化学势),电子将从费米能级高的N区流向费米能级低的P区,空穴则由p区流向n区,因此,$E_{Fn}$不断下移,$E_{Fp}$不断上移,直到相等为止。可以画出下面的图:
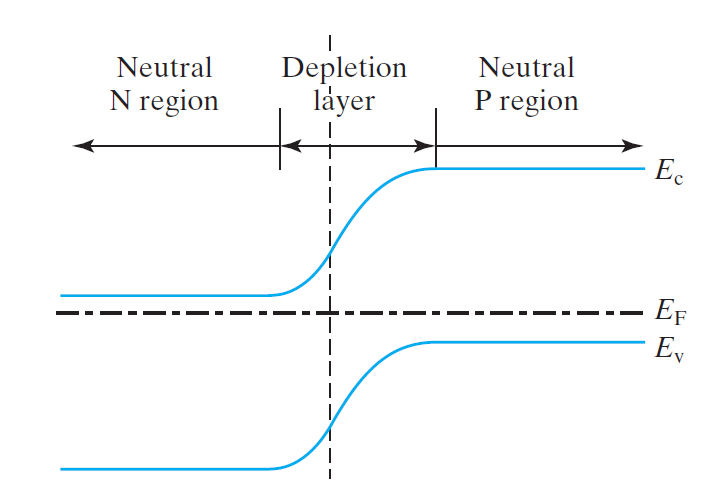
可以发现,在空间电荷区发生了能带弯曲,并且两边的导带和价带也发生了移动。弯曲的原因就是因为内建电场。根据物理知识,沿着电场方向电势降低,那么沿着电场方向电子的电势能将升高,所以p区的能带相对n区上移。
这个弯曲我们也可以这样形象的理解,只考虑电子。N区导带中电子有很多,如下图所示,从n区到p区没有任何阻碍,电子顺利的进入到了p区,这就是扩散运动。

但是由于内建电场,存在漂移运动,就阻碍电子运动到p区,那么怎么阻碍呢?很显然将表现为给你增加一堵墙,不让电子过去。如下图所示。这是最下面那一层电子因为有个墙堵着,就不能运动到p区了。这就是内建电场和漂移运动让能带表现出的弯曲效果。这样看是不是很直观很好理解?
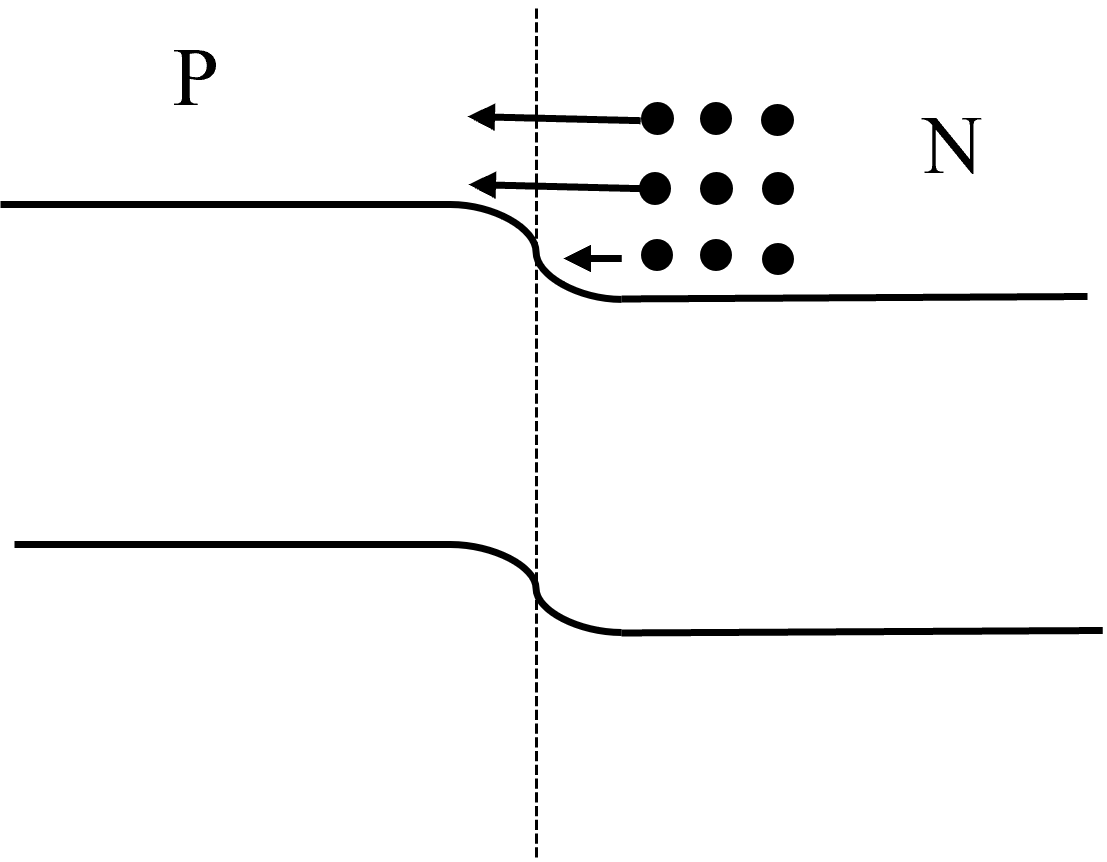
当最后达到平衡状态后,能带的弯曲使得N区的电子就都无法运动到P区。这个墙被称为势垒。电子需要越过势垒,才能从n区到达p区,故空间电荷区也称为势垒区。从上面那个解释中,我们也可以直观的看到,如果n区掺杂浓度越高,那么电子数目更多,则需要更高的墙才能阻碍所有电子运动到p区,故势垒增加。
势垒高度
平衡PN结的空点电荷区两端间的电势差$V_D$称为PN结的接触电势差或内建电势差,相应的电子电势能之差即能带的弯曲量$qV_D$称为PN结的势垒高度。
在之前的讨论中,势垒高度正好补偿了n区和p区费米能级之差,使得平衡pn结的费米能级处处相等。因此
$$
qV_D=E_{Fn}-E_{Fp}
$$
而如果n区和p区的掺杂浓度已知,那么可以求出它们的费米能级,也就能够求出势垒高度了。大家可以自行推导一下。
载流子分布
无论是研究电流、电容,都需要知道器件的载流子分布。因此,不论是什么半导体器件,载流子分布都是最重要的。其计算方法与前面计算N型或P型半导体的计算方法一样,都是状态密度乘分布函数。不考虑简并等因素,只研究空间电荷区,此时计算的过程与前面几乎是一样的,只不过E不再是一个恒定的值了,而是一个随着x变化的函数。因此,把之前公式里的E换成E(x),可以得到:
$$
n(x)=N_cexp(\frac{E_F-E(x)}{k_0T})
$$
然后就是对这个式子进行变换,换成我们容易分析的形式。利用$E(x)=-qV(x),n_{n0}=N_cexp(\frac{E_F-E_{cn}}{k_0T})$,可以化简成
$$
n(x)=n_{n0}exp(\frac{qV(x)-qV_D}{k_0T})
$$
有两个点的电子浓度我们需要知道,一个是空间电荷区靠近n区的边界处,此时电子浓度就是$n_{n0}$,而在空间电荷区靠近p区的边界处,我们知道其$E_C$变化了一个势垒高度,是不是很类似与之前讲到的两个掺杂不同的半导体,电子浓度差$exp(\frac{\Delta E_F}{k_0T})$(到这里我们可以发现,这是一个很方便我们分析的技巧,一定要记住),在这里,$E_F$没变,但是$E_C$变了,依旧可以套用,比$n_{n0}$变化了$exp(\frac{\Delta E_C}{k_0T})$,即电子浓度为$n_{n0}/exp(\frac{qV_D}{k_0T})=n_{n0}exp(-\frac{qV_D}{k_0T})$。
从这个式子我们可以发现:在空间电荷区靠近n区的边界处,此时电子浓度就等于其未与p区接触时的电子浓度,然后沿着空间电荷区,电子浓度成指数型减少。因此,我们发现,进入到空间电荷区后,电子会指数型减少,因此减少的特别快,所以在空间电荷区的大部分区域,其电子浓度都远远小于$n_{n0}$,我们也可以通过计算来描述这个现象,书中写到了在势垒区内电势能比n区导带底$E_{cn}$高$0.1eV$的点x处,电子浓度约为n区的$\frac{1}{50}$,空穴浓度约为p区的$10^{-10}$倍。因此,对于绝大部分势垒区,载流子浓度都远小于两侧的多子浓度,这就好像是这个区域耗尽了,没有载流子了。因此,这个区域又称为耗尽区。
但是要注意的是,耗尽区并非是没有载流子,载流子浓度可能有$10^{15}$,甚至更高,但两侧多子浓度可能为$10^{18}$,相比于多子浓度,耗尽区的载流子可以忽略不计。
空间电荷区,势垒区,耗尽区
讲到这里,我们可以发现空间电荷区、势垒区、耗尽区是指的同一个区域,但是并不能将它们混为一谈。它们每一个都有其含义,一定要对理解每个名字背后的含义。
空间电荷区是从空间电荷的角度来描述的,回顾一下空间电荷,空间电荷指的是那些起到正电或负电作用的正电中心和负电中心,由于载流子移动的时候,带电中心不可动,故导致了空间电荷的产生,从而导致了内建电场的形成。
势垒区是从能带的角度看待这个区域,由于内建电场,电子从n区到p区需要越过一个势垒。
耗尽区是从载流子的浓度方面看的,载流子浓度相比于两边的多子浓度很小,可以忽略,表现出了耗尽的特性,故称耗尽区。
这也是耗尽区最重要的三个特性:内建电场、势垒、耗尽。
电势、电场分布
电场分布
PN结包含了电场,使得电势发生了改变,因此需要研究其电场电势分布。这就引入了半导体物理的两大方程中的第二个,第一个是前面讲过的连续性方程,第二个就是泊松(Poisson)方程。这两个方程关系着半导体物理中最关心的参数,即载流子分布和电场/电势分布。
泊松方程如下:
$$
\frac{\mathrm{d}^2 V}{\mathrm{~d} x^2}=-\frac{\mathrm{d} \mathscr{E}}{\mathrm{d} x}=-\frac{\rho}{\varepsilon_s}
$$
这个方程可以有高斯定理推出,感兴趣可以去推一下,网上很容易找到。
在下面的分析中,都是在耗尽层近似的条件下进行的。在教材中,耗尽层近似有很多个条件,可以去看一下,在我看来,这个近似有一个核心,就是忽略耗尽区的载流子的作用。如果不存在载流子,则说明耗尽区电阻无穷大,则外界电压都降落在耗尽区上。不考虑载流子,也就相应的不考虑耗尽区内的产生和复合了。
建立坐标系,在这里我们将P区放在正半轴,其耗尽区对应于$0\ll x \ll x_P$,N区放在负半轴,耗尽区对应于$x_N\ll x \ll 0$ 。求解泊松方程,我们需要知道$\rho$,即电荷密度。在耗尽区近似后,认为耗尽区内的电荷就是空间电荷。因此,先考虑耗尽区内靠近P区的部分$0\ll x \ll x_P$:
$$
\rho=-qN_a
$$
首先求电场,将这个电荷密度带入得:
$$
-\frac{\mathrm{d} \mathscr{E}}{\mathrm{d} x}=-\frac{-qN_a}{\varepsilon_s}
$$
边界条件为耗尽区边界处电场为0,可以得到电场的表达式:
$$
\mathscr{E}(x)=-\frac{q N_{\mathrm{a}}}{\varepsilon_s} x+C_1=\frac{q N_{\mathrm{a}}}{\varepsilon_s}\left(x_{\mathrm{P}}-x\right) \quad 0 \leq x \leq x_{\mathrm{P}}
$$
可以发现这是一个线性分布,并且在$x=0$处达到最大值。当然,这也是很容易想到的,因为电荷密度为常数,那么积分后就是线性分布。
同理可得n区的电场分布:
$$
\mathscr{E}(x)=-\frac{q N_{\mathrm{d}}}{\varepsilon_s}\left(x-x_{\mathrm{N}}\right) \quad x_{\mathrm{N}} \leq x \leq 0
$$
电场是连续的,所以当$x=0$时,上面的两个式子相等,可以得到一个十分重要的结论:
$$
N_{\mathrm{a}}\left|x_{\mathrm{P}}\right|=N_{\mathrm{d}}\left|x_{\mathrm{N}}\right|
$$
根据这个式子,我们可以发现,n区和p区的耗尽区宽度与对应的掺杂浓度成反比,这就告诉我们了一个重要的现象:对于PN结,掺杂浓度更高的区域,耗尽区宽度更窄。在后面我们会经常的应用这个结论。这也引出了一个特例,假如有一边掺杂特别大,那么可以认为耗尽区几乎都处于轻掺杂的那边,这就是常用的N+P结或P+N结,即单边突变结,此时耗尽区宽度只受轻掺杂区域的掺杂浓度影响。
电势分布
电场积分后是电势,故可以猜测电势是二次分布。根据$\mathscr{E}=-dV/dx$,可以求出电势的表达式,如下:
$$
V(x)=-\frac{q N_{\mathrm{a}}}{2 \varepsilon_s}\left(x_{\mathrm{P}}-x\right)^2 \quad 0 \leq x \leq x_{\mathrm{P}}
$$
$$
\begin{aligned}
V(x) &=D-\frac{q N_{\mathrm{a}}}{2 \varepsilon_s}\left(x-x_{\mathrm{N}}\right)^2 & & \\
&=\phi_{\mathrm{bi}}-\frac{q N_{\mathrm{d}}}{2 \varepsilon_s}\left(x-x_{\mathrm{N}}\right)^2 & x_{\mathrm{N}} \leq x \leq 0
\end{aligned}
$$
可以在坐标系中画出电场和电势的分布图,图来源于《Modern Semiconductor Devices for Integrated Circuits》,如下:
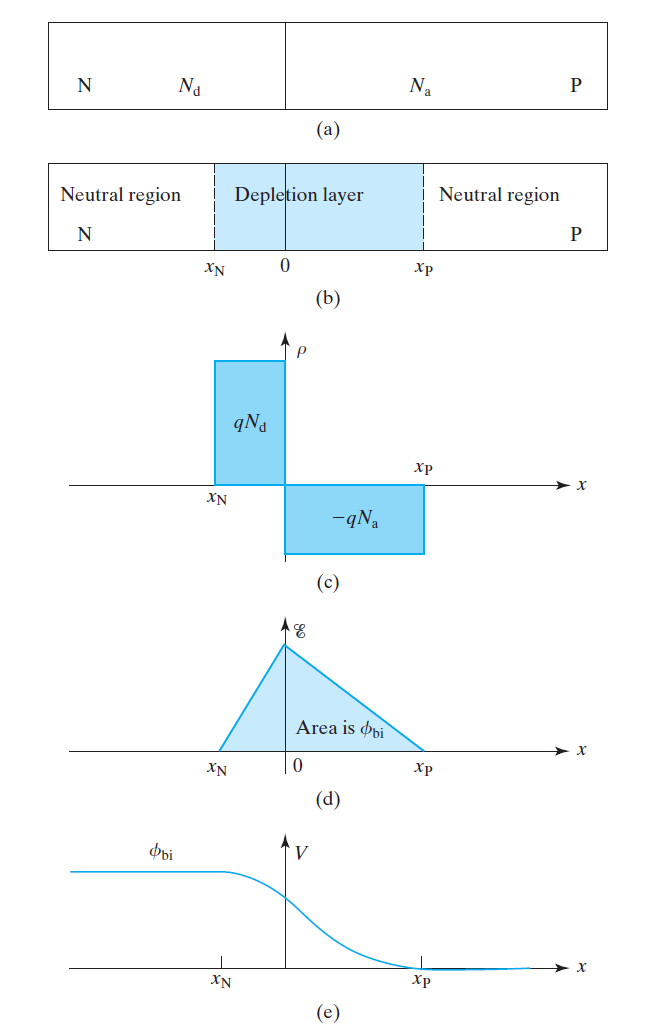
同电场一样,电势也是连续的,在$x=0$处相等,故可以得到:
$$
\frac{qN_a}{2\varepsilon_s}x_P^2=\phi_{\mathrm{bi}}-\frac{q N_{\mathrm{d}}}{2 \varepsilon_s}x_{\mathrm{N}}^2
$$
耗尽区宽度
耗尽区宽度为$W_{dep}=x_P-x_N$。根据上面的公式,联立:
$$
N_{\mathrm{a}}\left|x_{\mathrm{P}}\right|=N_{\mathrm{d}}\left|x_{\mathrm{N}}\right|
$$
$$
\frac{qN_a}{2\varepsilon_s}x_P^2=\phi_{\mathrm{bi}}-\frac{q N_{\mathrm{d}}}{2 \varepsilon_s}x_{\mathrm{N}}^2
$$
得:
$$
x_{\mathrm{P}}-x_{\mathrm{N}}=W_{\mathrm{dep}}=\sqrt{\frac{2 \varepsilon_s \phi_{\mathrm{bi}}}{q}\left(\frac{1}{N_{\mathrm{a}}}+\frac{1}{N_{\mathrm{d}}}\right)}
$$
观察这个式子,可以看到耗尽区宽度与势垒高度正相关,与掺杂浓度负相关。其中,观察掺杂浓度的项,这个形式就很像电阻并联的公式,我们在记忆的时候也可以这么记。以并联电阻的求法求出一个等效浓度$N$,然后可以得到下面这个形式:
$$
W_{\mathrm{dep}}=\sqrt{\frac{2 \varepsilon_s \phi_{\mathrm{bi}}}{qN}}
$$
这样是不是就好记多了。
考虑单边突变结这种特殊情况,对于N+P,$N_d>>N_a$,故等效浓度约为$N_a$,则
$$
W_{\mathrm{dep}}=\sqrt{\frac{2 \varepsilon_s \phi_{\mathrm{bi}}}{qN_a}}
$$
可以发现耗尽区宽度由轻掺杂的一方决定。
势垒区电容
在势垒区中,几乎不存在载流子,类似于一个绝缘体,但又存在内建电场,因此可以等效为一个平行板电容器。
$$
C_{\mathrm{dep}}=A \frac{\varepsilon_s}{W_{\mathrm{dep}}}
$$
将耗尽区宽度的公式代入进去,可以得到电容的公式:
$$
C_{dep}=A\sqrt{\frac{qN\varepsilon _s}{2\phi_{\mathrm{bi}}}}
$$
到这里,平衡状态下PN结涉及到的知识差不多就讲完了。下面就是将PN结的重点——外加电压下的PN结。当外加电压后,PN结的平衡状态被打破,又会发生什么呢?










物理系本科生路过,文章简洁明了,推导深入浅出,赞!
谢谢~