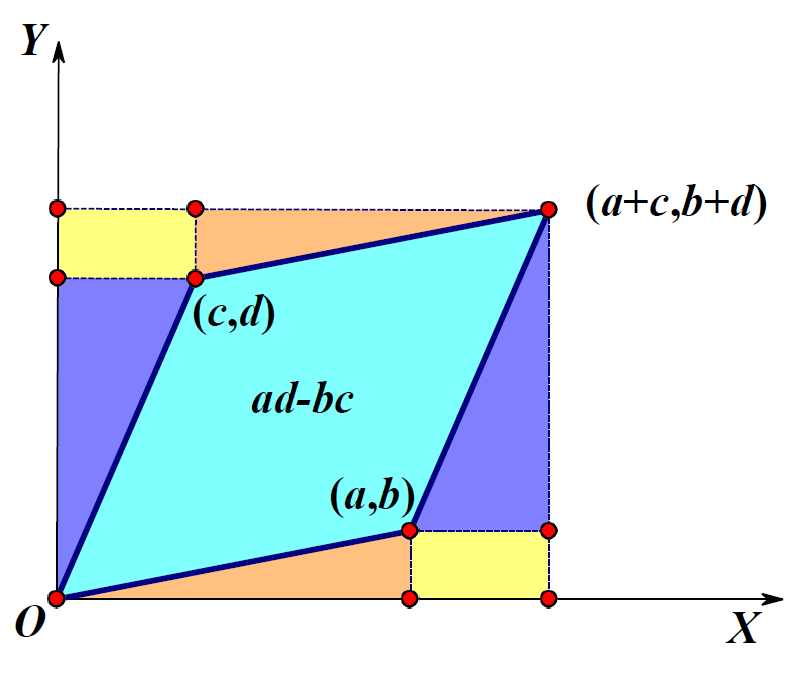
线性变换的作用
我们再来仔细的看一下基向量的转换。每对不同的基向量都对应着一个不同的空间,为了方便说明问题,我们以两个人的视角来表示这两个空间,我们所在的空间对应平面直角坐标系,而另一个人小明所在的空间对应着另外一组基向量对应的空间。那么显然,对于一个向量,比如$\begin{bmatrix} 1 \\ 2 \end{bmatrix}$,在我们和小明的视角里,看到的向量并不相同。
那么,我们知道,不同坐标系之间是可以通过线性变换转换的。假如站在我们的视角,小明所看到的基向量坐标分别为$\begin{bmatrix} -1 \\ 0 \end{bmatrix}$和$\begin{bmatrix} 3 \\ 1 \end{bmatrix}$,考虑小明视角中的向量$\begin{bmatrix} 1 \\ 2 \end{bmatrix}$,在我们的视角里应该是多少呢?
很明显,通过换算就可以得到结果,如下:
$$
1\begin{bmatrix} -1 \\ 0 \end{bmatrix}+2\begin{bmatrix} 3 \\ 1 \end{bmatrix}=\begin{bmatrix} 5 \\ 2 \end{bmatrix}
$$
我们将其写成矩阵乘法:
$$
\begin{bmatrix} -1&3 \\ 0&1 \end{bmatrix}\begin{bmatrix} 1 \\ 2 \end{bmatrix}=\begin{bmatrix} 5 \\ 2 \end{bmatrix}
$$
这个看似是将我们之前在谈矩阵的时候,又重复了一遍。但是从我们现在考虑问题的角度来看待这个问题,通过这个式子,这个矩阵将小明视角里的向量$\begin{bmatrix} 1 \\ 2 \end{bmatrix}$转换成了我们视角里的$\begin{bmatrix} 5 \\ 2 \end{bmatrix}$,这句话的意思不是说这个向量发生了改变,而是用向量未变,而是视角转变,用我们的视角看待小明空间中的向量。小明视角里的$\begin{bmatrix} 1 \\ 2 \end{bmatrix}$在我们的视角里就是$\begin{bmatrix} 5 \\ 2 \end{bmatrix}$。这表明矩阵乘法是将这个矩阵对应的空间中的向量翻译到我们的视角。
这个角度是与之前不同的,在之前我们是这样看待线性变换的:这个矩阵是将我们视角里的向量变换到另一个空间中。这就是线性变换的两个含义:
- 将我们视角中的向量变换到另一个空间,向量转换:Our grid -> Ming's grid
- 用我们空间中的坐标表示小明视角里的向量,视角转换:Our language <- Ming's language

这两个过程是相反的。视角转换是很重要的,一定要理解。
为了更好的理解,再换个方法来说明这个问题,看完下面这个,你应该能理解的更加透彻。
在这其中,其实就是涉及到两个东西,分别是向量和视角。视角的转换可以通过矩阵乘法进行,矩阵是由基向量构成的。线性变换涉及到两个,一个从我们的空间转换到小明的空间,一个是小明的空间转换到我们的空间。这两个变换其实就是我们视角中的小明空间的基向量以及小明视角中的我们空间的基向量。
再来看线性变换,对于一个小明空间中的向量,乘以变换矩阵,得到这个向量在我们空间的表示。可以写成下面这句话:
vector in his language * his basis in our language = vector in our language (his basis in his language = 1)
得到的结果是向量未变,视角改变。
那么如果对于我们空间中的一个向量,想知道小明空间看到的是多少,那应该怎么写呢?
vector in our language * our basis in his language = vector in his language
其中our basis in his language就对应着矩阵的逆。
再来看前几章的向量转换,用这种方式写一下,那就是:
vector in our language * his basis in our language = new_vector in our language
其中new_vector = vector * his basis in our language
因此,向量发生了变化,视角没有改变。
到此,我们看待线性变换就有了两个角度,一定要充分理解,不要搞混。
一个问题
接下来,我们利用线性变换的两个含义来思考下面的问题,这个问题同时用到了线性变换的两个含义,弄明白之后,你就大致理解了线性变换。
假如站在我们的视角里,对坐标系施加一个向左旋转90°的变换,根据前文知识,我们可以知道其对应的矩阵为:
$$
M=\begin{bmatrix} 0&1 \\ -1&0 \end{bmatrix}
$$
考虑这么一个问题,在小明的视角里,对坐标系施加一个向左旋转90°的变换,他看到的变换矩阵是什么?或者说在小明的视角中,找到一个矩阵,让这个矩阵乘以他空间中的向量,使得这个向量向左旋转了90°。接下来我们一步步分析,注意视角的转换:
- 假设小明视角里有一个向量$\vec{v}$,先转换为我们的视角,即视角转换,我们看到的向量为$A\vec{v}$。此时是向量未变,视角改变。
- 然后进行旋转操作,这个是向量转换,对我们空间中的向量线性变换,得到$MA\vec{v}$,此时还是站在我们的视角里,因为此时线性变换的作用为向量改变,视角不变;
- 然后再进行视角转换。此时小明看到的向量变为了$A^{-1}MA\vec{v}$,此时在小明看来,已经完成了向左旋转90°的操作。因此,小明看到的旋转矩阵就是$A^{-1}MA$。这个过程也可以描述成这样:
vector in his language * his basis in our language * transformation in our language * our basis in his language = vector_transformation in his language
这个结论也是十分重要的,因为这个式子表明了线性变换的映射,将一个空间中的线性变换映射到另一个空间。