前言

推荐先去看主成分分析 这篇文章，本篇内容与这篇文章思想一致。

今天听耿修瑞老师讲了他提出的协偏度张量和主偏度分析（PSA）方法，我收获满满，以至于想立刻把学到的东西记录下来。同时也看到了他发的一篇博文，链接如下： https://blog.sciencenet.cn/home.php?mod=space&uid=528211&do=blog&id=847749 ，讲述了他发表 PSA 时的曲折经历，感慨一个新的理论发表是多么的不容易，也敬佩老师的创新精神，讲 PCA 的思想引入独立成分分析。也希望自己能够向老师学习，勤加思考。如果有对 PSA 感兴趣的，可以去看耿修瑞老师发表的文章，相信你一定会受益匪浅的。

问题背景

生活中，常常会遇到信号叠加的问题，比如一段音频，可能是多个音频的叠加，再比如一张图片，可能是多张图片的叠加。再比如说，在通信过程中，接收到的信号可能会是通信源和干扰源的叠加。在这种情况下，我们就需要根据这些叠加后的信号，来分离出原来独立的信号，这就是独立成分分析。

假设现在有三个不同的叠加后的图像 $\mathbf{X_1},\mathbf{X_2},\mathbf{X_3}$，我们希望得到原先的图像 $\mathbf{s_1},\mathbf{s_2},\mathbf{s_3}$。这是一个线性方程组，如果我们知道这些系数，那么可以直接得到结果。但是问题是我们并不知道这些线性组合的系数，因此，需要找寻另外的方法。

$$
\begin{matrix}
\mathbf{X_1}=a_{11}\mathbf{s_1}+a_{12}\mathbf{s_2}+a_{13}\mathbf{s_3} \\
\mathbf{X_2}=a_{21}\mathbf{s_1}+a_{22}\mathbf{s_2}+a_{23}\mathbf{s_3} \\
\mathbf{X_3}=a_{31}\mathbf{s_1}+a_{32}\mathbf{s_2}+a_{33}\mathbf{s_3}
\end{matrix}
$$

在主成分分析中，我们是需要对高维数据提取出主要特征，也就是找到具有最大信息量的方向。我们在解决这个问题中，采取的办法是，找到一个评判指标，我们已经知道了这个评价指标就是方差，然后探究求解方法，最后得到了一个解析表达式，从而知道了求解的方法。

在这里，我们是不是也可以采用同样的方法呢？当然是可以的，接下来我们就尝试按照这个步骤，一步步的求解这个问题。

评价指标

对于这个问题，显然方差是没办法的。在概率论中，我们曾学过中心极限定理，即大量相互独立随机变量的均值经适当标准化后依分布收敛于标准正态分布。简单来说，多个独立随机变量的和会收敛于高斯分布。那么，我们是不是可以从中得到一些启示呢？

对于原先的图像 $\mathbf{s_1},\mathbf{s_2},\mathbf{s_3}$，可以看作是一组独立随机变量，当对它们进行线性组合后，那么得到的图像，将会比原图像更加趋于高斯分布，即“高斯性”增强。那么反过来，如果我们想恢复到原图像，那么可以对叠加后的图像 $\mathbf{X_1},\mathbf{X_2},\mathbf{X_3}$，进行线性组合，使其“高斯性”减弱，或者说是“非高斯性”增强。那么用什么指标来衡量“高斯性”呢，也就是偏离高斯分布的程度？

这个指标就是偏度（skewness）或者峭度 (kurtosis)。如下图所示：

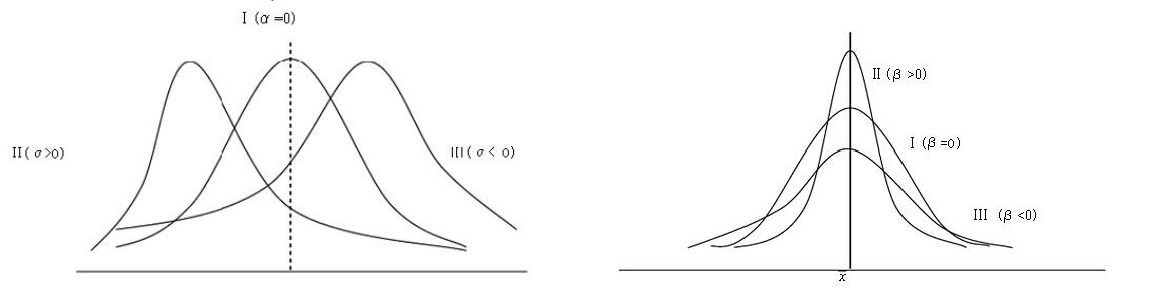
在左图中，中间的曲线为标准的高斯分布，可以发现，两边的曲线分别向两个方向偏离了高斯分布，而偏度就是描述了这个偏离的程度。其中，如果向左边偏，那么偏度大于 0。在右图中，中间的曲线为高斯分布，上下两条曲线分别比高斯分布更加陡峭和平缓，描述陡峭程度的量就是峭度。

这时，就搞定了解决这个问题的第一步，那就是对 $\mathbf{Y}=u_1\mathbf{X_1}+u_2\mathbf{X_2}+u_3\mathbf{X_3}$，找到 $\mathbf{u}=[u_{1}\quad u_{2}\quad u_{3}]$，使得 $\mathbf{Y}$ 的偏度或峭度足够大，

偏度和峭度计算方法

偏度

$$
\operatorname{Skewness}(\mathbf{x})=\frac{E\left(x_i-\bar{x}\right)^3}{\sigma^3}=\frac{\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^3}{\operatorname{Var}(\mathbf{x})^{3 / 2}}
$$

峭度

$$
\operatorname{Kurtosis}(\mathbf{x})=\frac{E\left(x_i-\bar{x}\right)^4}{\sigma^4}-3=\frac{\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^4}{\operatorname{Var}(\mathbf{x})^2}-3
$$

可以发现，偏度是单个随机变量的三阶统计量，峭度是单个随机变量的四阶统计量。与方差相同，针对的是单特征数据，也就是我们只能说数据在某个方向投影后的偏度是多少。

由于偏度是三阶统计量，较峭度比较简单，且偏度描述的是偏离程度，因此，接下来就采用偏度作为评价指标。

先看主成分分析中的那个例子。对于平面中均匀分布的散点，我们可以很容易知道这些点在任意方向上的偏度都是 0，因为无论在哪个方向的投影，投影后都是对称的，并不偏。从计算式中也可以看出，其计算中包含三次方，对于对称的点，在计算时会抵消掉，所以偏度为 0.

假设数据中存在异常点，异常点对方差几乎没有影响，也就是对二阶统计量几乎没有影响，但是对于高阶统计量影响很大，比如偏度和峭度。因此，可以利用高阶统计量，来检验异常点。

穷举法求偏度极值

对于这个问题，最容易想到的就是利用穷举法，随机找一些方向，然后求投影 $\mathbf{u}^T\mathbf{X}$，然后利用公式计算其偏度，找到一个最大的方向。

通过这种方法，首先得到了一个方向 $\mathbf{u_1}$，可以利用这个方向求出第一个独立成分。那么如何求另外两个成分呢？可以利用正交投影矩阵。

找到一个 $\mathbf{u_1}$ 后，求出其正交补投影矩阵 $\mathbf{P_1}=\mathbf{I}-\mathbf{u_1}\mathbf{u_1}^\#=\mathbf{I}-\mathbf{u_1}\mathbf{u_1}^T$，将原数据投影到该方向的正交补空间中，即令 $\mathbf{X}=\mathbf{P_1X}$，通过这种方式，就将原数据删除了第一个独立成分，也就是此时的 $\mathbf{X}$ 只是两个独立成分的叠加。然后再利用穷举法，得到第二个方向 $\mathbf{u_2}$，从而得到第二个独立成分，然后利用相同的方法，得到第三个独立成分。在这个过程中，利用了两次穷举法。

虽然穷举法也能得到一个相对不错的解，但是穷举法具有很多的不确定性，这肯定不是我们理想中的方法。

任意方向的偏度计算

分析

在主成分分析中，我们得到了任意方向上的方差的解析表达式，从而使得求解变得十分简单。那么能不能在独立成分分析中，也能够得到一个解析表达式呢？

在主成分分析中，其解析表达式是一个十分简洁的形式，即 $\mathbf{u}^T \Sigma \mathbf{u}$，这个式子说明了一个很重要的事情，也就是协方差矩阵包含了所有方向的方差信息，然后利用 $\mathbf{u}^T \Sigma \mathbf{u}$ 将协方差对应方向中的方差提取出来。那么，类似的，我们能不能找到一个包含所有方向上的偏度信息的“矩阵”呢？继续类比，方差是二阶统计量，对应的是矩阵，那么偏度是三阶统计量，对应的还会是矩阵吗？答案是不是的，将会是更加复杂的结构，那就是三阶张量。可以发现这是一个很妙、也是很自然的扩展，方差对应的矩阵是二阶张量，偏度对应的恰好是三阶张量。

在这里，张量这个概念可能难以理解一些，可以用多维数组来理解它，学过编程的人对多维数组应该很不陌生。三阶张量，就是一个具有三个维度的数据立方体。

再看主成分分析的过程，第一步是进行数据中心化，其目的就是对方差的表达式 $\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2$，括号里的内容进行简化。再看偏度的计算公式：

$$
\operatorname{Skewness}(\mathbf{x})=\frac{E\left(x_i-\bar{x}\right)^3}{\sigma^3}=\frac{\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^3}{\operatorname{Var}(\mathbf{x})^{3 / 2}}
$$

可以看到，我们依然可以使用数据中心化的方法，对括号里的内容进行简化。但是，偏度的计算公式中，还有一个分母，那么能不能通过一个变换，把分母去掉呢？答案是可以的。

数据的白化

将分母去掉，也就是通过一个变化，让变换后的矩阵的方差变为 1，并且使协方差变为 0，那么就是让协方差矩阵变为单位矩阵。令白化算子为 $\mathbf{F}$，接下来求这个白化算子。

令 $\hat{\mathbf{X}}=\mathbf{F}^T\mathbf{X}$，$\hat{\mathbf{X}}$ 的协方差矩阵记为 $\hat{\mathbf{\Sigma}}$，下面进行计算：

$$
\begin{aligned}
\hat{\mathbf{\Sigma}}&=\frac{1}{N}\hat{\mathbf{X}}\hat{\mathbf{X}}^{T}\\
&= \frac{1}{N}\mathbf{F}^T\mathbf{X}\mathbf{X}^{T}\mathbf{F}
\end{aligned}
$$
对原矩阵的协方差矩阵进行分解，即 $\frac{1}{N}\mathbf{X}\mathbf{X}^T=\mathbf{U}\mathbf{D}\mathbf{U}^T$。然后继续进行计算：

$$
\begin{aligned}
\hat{\mathbf{\Sigma}}&=\frac{1}{N}\hat{\mathbf{X}}\hat{\mathbf{X}}^{T}\\
&= \frac{1}{N}\mathbf{F}^T\mathbf{X}\mathbf{X}^{T}\mathbf{F}\\
&= \mathbf{F}^T\mathbf{U}\mathbf{D}\mathbf{U}^{T}\mathbf{F}\\
&= \mathbf{F}^T\mathbf{U}\mathbf{D}^{\frac{1}{2}}\mathbf{D}^{\frac{1}{2}}\mathbf{U}^{T}\mathbf{F}\\
&= \mathbf{F}^T(\mathbf{U}\mathbf{D}^{\frac{1}{2}})(\mathbf{D}^{\frac{1}{2}}\mathbf{U}^{T})\mathbf{F}\\
&= \mathbf{I}
\end{aligned}
$$
从上式中可以求得，$\mathbf{F}=(\mathbf{D}^{\frac{1}{2}}\mathbf{U}^{T})^{-1}=\mathbf{U}\mathbf{D}^{-\frac{1}{2}}$。

对数据进行中心化和白化处理后，得到：

$$
\hat{\mathbf{X}}=\mathbf{F}^{\mathrm{T}} \mathbf{X}=\left[\begin{array}{c}
\hat{X}_1 \\
\vdots \\
\hat{X}_L
\end{array}\right]=\left[\hat{\mathbf{r}}_1, \hat{\mathbf{r}}_2, \cdots, \hat{\mathbf{r}}_N\right]
$$

$$
\mathbf{u}^{\mathrm{T}} \hat{\mathbf{X}}=\left[\mathbf{u}^{\mathrm{T}} \hat{\mathbf{r}}_1, \mathbf{u}^{\mathrm{T}} \hat{\mathbf{r}}_2, \cdots, \mathbf{u}^{\mathrm{T}} \hat{\mathbf{r}}_N\right]
$$

协偏度张量

接下来求偏度：

$$
\begin{aligned}
\text { Skewness }\left(\mathbf{u}^{\mathrm{T}} \hat{\mathbf{X}}\right)
&= \operatorname{Skewness}\left(\left[\mathbf{u}^{\mathrm{T}} \hat{\mathbf{r}}_1, \mathbf{u}^{\mathrm{T}} \hat{\mathbf{r}}_2, \cdots, \mathbf{u}^{\mathrm{T}} \hat{\mathbf{r}}_N\right]\right) \\
&= \frac{\frac{1}{N} \sum_{i=1}^N\left(\mathbf{u}^{\mathrm{T}} \hat{\mathbf{r}}_i-0\right)^3}{\operatorname{Var}\left(\mathbf{u}^{\mathrm{T}} \hat{\mathbf{X}}\right)^{3 / 2}} \\
&= \frac{1}{N} \sum_{i=1}^N\left(\mathbf{u}^{\mathrm{T}} \hat{\mathbf{r}}_i\right)^3 \\
&=\left(\frac{1}{N} \sum_{i=1}^N\left(\hat{\mathbf{r}}_i \circ \hat{\mathbf{r}}_i \circ \hat{\mathbf{r}}_i\right)\right)\times_1 \mathbf{u} \times_2 \mathbf{u} \times_3 \mathbf{u} \\
&= \underline{\mathbf{S}} \times_1 \mathbf{u} \times_2 \mathbf{u} \times_3 \mathbf{u}
\end{aligned}
$$

上面的 $\circ$ 为外积运算。这个 mode 乘积在行列式的含义 中大致介绍了一下，可以去看一下。

其中，$\underline{S}$ 称为协偏度张量。如何理解这个式子呢？我们可以先看二维的情况。

可以发现，这是一个十分自然的扩展。

协偏度张量具有三个方向，在任意方向的偏度就是用它的各个分量分别从三个方向对协偏度张量进行加权求和，如下图所示：

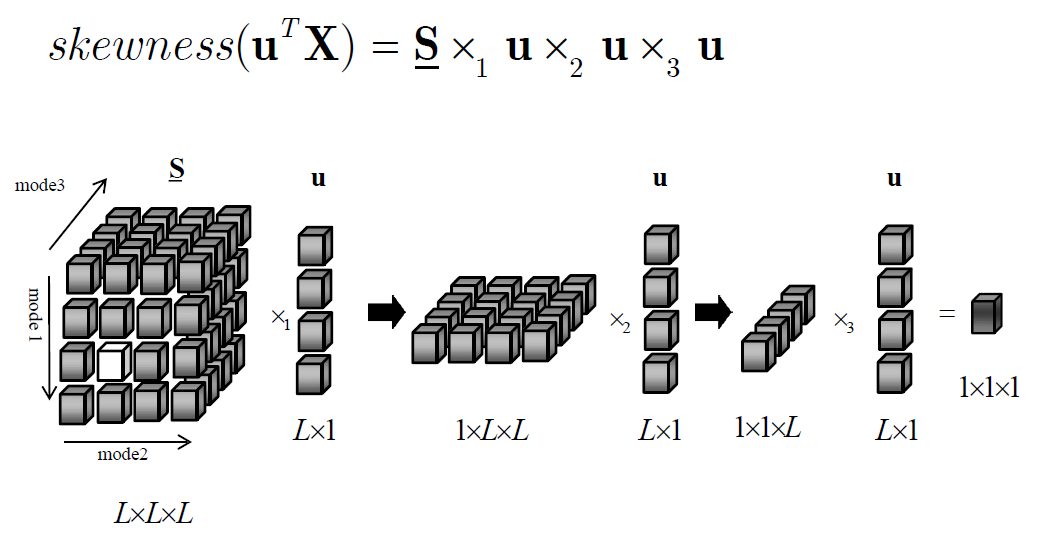
协偏度张量的计算

有两种方法，也就是分别从两个角度看待这个计算问题。

外积法（列向量角度）

$$
\underline{\mathbf{S}}=\frac{1}{N} \sum_{i=1}^N \hat{\mathbf{r}}_i^3=\frac{1}{N} \sum_{i=1}^N \hat{\mathbf{r}}_i \circ \hat{\mathbf{r}}_i \circ \hat{\mathbf{r}}_i
$$

内积法（行向量角度）

$$
\begin{aligned}
& s_{i j k}=\frac{1}{N} \sum_{l=1}^N \hat{X}_i(l) \hat{X}_j(l) \hat{X}_k(l) \\
& s_{i j k}=s_{i k j}=s_{j i k}=s_{j k i}=s_{k i j}=s_{k j i}
\end{aligned}
$$

有了协偏度张量，就引出了独立成分分析的一种方法，也就是主偏度分析（PSA）。

主偏度分析

模型：

$$
\begin{aligned}
& \max g(\mathbf{u})=\underline{\mathbf{S}} \times_1 \mathbf{u} \times_2 \mathbf{u} \times_3 \mathbf{u} \\
& \text { s.t. } \mathbf{u}^T \mathbf{u}=1
\end{aligned}
$$

利用拉格朗日乘子法，可以得到解：

$$
\underline{\mathbf{S}} \times_1 \mathbf{u} \times_3 \mathbf{u}=\lambda \mathbf{u}
$$

这个求解是很复杂的，协偏度张量的特征对个数很多，目前好像还没有很好的求解方法。但是，我们可以利用固定点法，求出其中的一个特征对，也就是其中的一个方向。

固定点法就是计算如下式子：

$$
\begin{aligned}
\mathbf{u} & =\underline{\mathbf{S}} \times_1 \mathbf{u} \times_3 \mathbf{u} \\
\mathbf{u} & =\frac{\mathbf{u}}{|\mathbf{u}|}
\end{aligned}
$$

通过计算，可以得到 $\mathbf{u_1}$ ，从而得到了第一个独立成分。那么如何得到第二个独立成分呢？共有三种方法。

正交投影法

也就是计算 $\mathbf{u_1}$ 的正交投影矩阵，然后对原张量进行投影，去掉原张量关于第一个成分的信息，然后再利用固定点法，求出第二个方向。

$$
\begin{aligned}
& \mathbf{P}_1=\mathbf{I}-\mathbf{u}_1 \mathbf{u}_1^{\#}, \quad \mathbf{X}_1=\mathbf{P}_1 \hat{\mathbf{X}} \\
& \underline{\mathbf{S}}_1=\frac{1}{N} \sum_{i=1}^N\left(\mathbf{P}_1 \hat{\mathbf{r}_i}\right)^3=\frac{1}{N} \sum_{i=1}^N \mathbf{P}_1 \hat{\mathbf{r}_i} \circ \mathbf{P}_1 \hat{\mathbf{r}_i} \circ \mathbf{P}_1 \hat{\mathbf{r}_i} \\
& =\underline{\mathbf{S}} \times_1 \mathbf{P}_1 \times_2 \mathbf{P}_1 \times_3 \mathbf{P}_1 \\
& \mathbf{u}=\underline{\mathbf{S}}_1 \times_1 \mathbf{u} \times_3 \mathbf{u}
\end{aligned}
$$

Deflation 法

$$
\begin{aligned}
& \underline{\mathbf{S}}_1=\underline{\mathbf{S}}-\lambda \mathbf{u}_1 \circ \mathbf{u}_1 \circ \mathbf{u}_1 \\
& \mathbf{u}=\underline{\mathbf{S}}_1 \times_1 \mathbf{u} \times_3 \mathbf{u}
\end{aligned}
$$

Kronecker 法

$$
\begin{aligned}
& \mathbf{P}_1=\mathbf{I}-\left(\mathbf{u}_1 \otimes \mathbf{u}_1 \otimes \mathbf{u}_1\right)\left(\mathbf{u}_1 \otimes \mathbf{u}_1 \otimes \mathbf{u}_1\right)^{\#} \\
& \underline{\mathbf{S}}_1=\operatorname{tensor}\left(\mathbf{P}_1 \operatorname{vec}(\underline{\mathbf{S}})\right) \\
& \mathbf{u}=\underline{\mathbf{S}}_1 \times_1 \mathbf{u} \times_3 \mathbf{u}
\end{aligned}
$$

Deflation 法与 Kronecker 法等价，但是与正交投影法并不等价。

上述三种方法在主成分分析的形式

正交投影法：

$$
\begin{aligned}
& \mathbf{P}_1=\mathbf{I}-\mathbf{u}_1 \mathbf{u}_1^{\#}, \quad \mathbf{X}_1=\mathbf{P}_1 \mathbf{X} \\
& \Sigma_1=\frac{1}{N} \mathbf{X}_1 \mathbf{X}_1^{\mathrm{T}}=\mathbf{P}_1 \Sigma \mathbf{P}_1 \\
& =\mathbf{\Sigma} \times_1 \mathbf{P}_1 \times_2 \mathbf{P}_1 \\
& \Sigma_1 \mathbf{u}=\lambda \mathbf{u}
\end{aligned}
$$

Deflation 法：

$$
\begin{aligned}
& \Sigma_1=\Sigma-\lambda \mathbf{u}_1 \mathbf{u}_1^{\mathrm{T}} \\
& \Sigma_1 \mathbf{u}=\lambda \mathbf{u}
\end{aligned}
$$

Kronecker 法：

$$
\begin{aligned}
& \mathbf{P}_1=\mathbf{I}-\left(\mathbf{u}_1 \otimes \mathbf{u}_1\right)\left(\mathbf{u}_1 \otimes \mathbf{u}_1\right)^{\#} \\
& \Sigma_1=\operatorname{unvec}\left(\mathbf{P}_1 \operatorname{vec}(\Sigma)\right) \\
& \Sigma_1 \mathbf{u}=\lambda \mathbf{u}
\end{aligned}
$$

这三种方法是等价的。证明如下：

可以看到，这些方法对于二阶量等价，但是高阶量就不一定了。

初值问题

由于求解采用的是固定点法，并不像是 PCA 中，直接求了所有的特征值和特征向量。因此，固定点法的求解结果将与初值有关。这个会在后面的几何解释中也会得到体现。

主偏度分析步骤

预处理

1. 数据中心化
2. 计算协方差矩阵：$\Sigma=\frac{1}{N}\mathbf{X}\mathbf{X}^T$
3. 计算协方差矩阵的特征值和特征向量：$\Sigma \mathbf{U}=\mathbf{U} \Lambda$
4. 计算白化算子：$\mathbf{F}=\mathbf{U} \Lambda^{-1 / 2}$
5. 对数据进行白化：$\hat{\mathbf{X}}=\mathbf{F}^{\mathrm{T}} \mathbf{X}$
6. 计算协偏度张量：内积法/外积法

主偏度变换

1. 计算数据的第一极值偏度方向 $\mathbf{u_1}$：

$$
\begin{aligned}
\mathbf{u} & =\underline{\mathbf{S}} \times_1 \mathbf{u} \times_3 \mathbf{u} \\
\mathbf{u} & =\frac{\mathbf{u}}{|\mathbf{u}|}
\end{aligned}
$$

2. 利用正交投影法等消除第一个主偏度方向的影响
3. 计算新的协偏度张量：

$$
\underline{\mathbf{S}}_1=\underline{\mathbf{S}} \times{ }_1 \mathbf{P}_1 \times{ }_2 \mathbf{P}_1 \times_3 \mathbf{P}_1
$$

4. 再利用固定点法，求第二极值偏度方向

PSA 几何解释

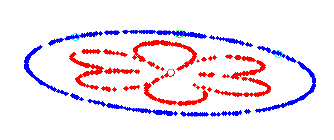
PCA 的几何结构是一个椭圆，PSA 的几何结构是一个类似于多个“花瓣”组成的图形，如下红色部分：

从这个几何结构中也能看出，当初值位于不同的“花瓣”时，将会收敛到对应“花瓣”的顶点。同时这也说明了，为什么有的时候会得到一个完全相反的结果，也就是乘了一个-1。这正好对应了“花瓣”的对称性，即在相反方向有一个相同的“花瓣”。