（长文预警，推荐看完）。在初学行列式时，只知道它是一个数，有着一些神奇的性质。对于行列式的计算，我们在学习时会接触到逆序数这个词，但是并不知道为什么会有这个逆序数。

下面我们就从几何意义与代数意义来更全面的了解行列式。

行列式的几何意义

考虑二维情况下，一个平面中有两个向量，分别为$(a,b),(c,d)$，那么这两个向量张成的平行四边形的面积是多少？

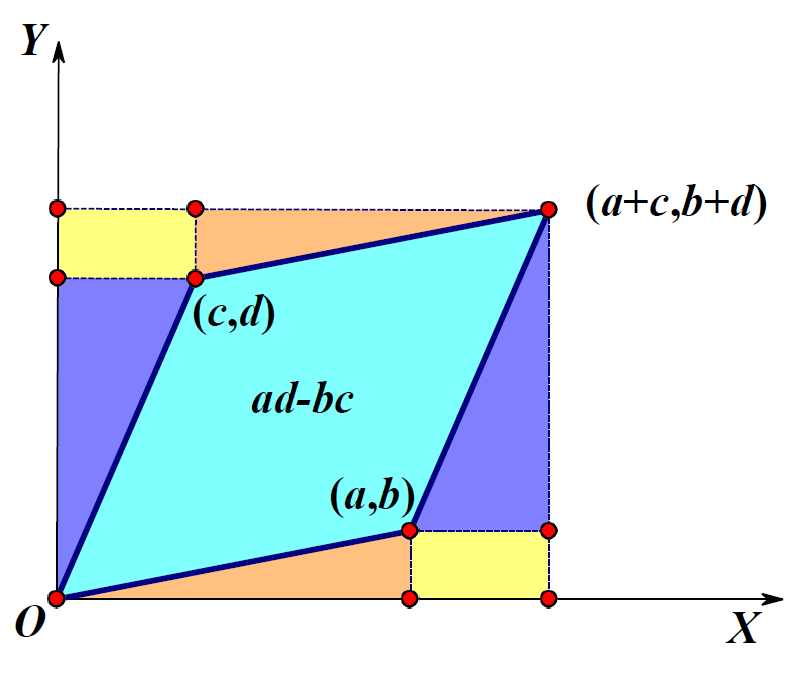
如上图所示，我们可以得出面积为：

$$
\begin{aligned}
S&= (a+c)(b+d)-ab-cd-2bc \\
&= ad-bc \\
&= \begin{vmatrix}
a & c \\
b & d
\end{vmatrix}
\end{aligned}
$$

可以看到，该平行四边形的面积恰好等于由这两个向量构成的矩阵的行列式。

那么三维情况呢？通过推导，我们可以知道，三维空间中，三个向量张成的平行四面体的体积恰好为该三个向量构成的矩阵的行列式。

因此，我们可以推测，n阶方阵的行列式的含义就是n个列向量张成的平行多面体的体积。这是一个很重要的结论，也是行列式的几何意义。

上面只是我们从二维情况和三维情况推测出的结论，那么有没有办法证明呢？

行列式几何意义的证明

有关这个问题，我参考了这个网站，自己总结了一下，如下：

我们先考虑二维情况，对于随便给出的两个向量，组成的平行四边形是很难求的。那么我们可以考虑将平行四边形变换成矩形，同时保持体积不变。我们先考虑如何变换，才能使得体积不变。

这个问题还是很简单的，其中一个向量均有相比于另一个分量的垂直分量和水平分量，而水平分量并不对面积或体积做出贡献。也就是说，对于两个向量$\mathbf{a},\mathbf{b}$，假设$\mathbf{a}$在$\mathbf{b}$上的分量为$\mathbf{a}_\perp$，因为只有垂直分量才对面积或体积做出贡献，所以$|\mathbf{a}\ \ \mathbf{b}|=|\mathbf{a_\perp}\ \ \mathbf{b}|$。那么对于$\mathbf{a}-c\mathbf{b}$，不论常数$c$为多少，第二项相比于$\mathbf{b}$的垂直分量均为0，因此，在进行$\mathbf{a}$到$\mathbf{a}-c\mathbf{b}$的变换后，平行四边形的面积不变。显然，这个结论是可以推广到更高维度的。即如果再有一个向量$\mathbf{c}$，有着相对于$\mathbf{a},\mathbf{b}$张成的平面的垂直分量和水平分量，水平分量并不影响体积，那么当$\mathbf{c}$变换到$\mathbf{c}-c_1\mathbf{a}-c_2\mathbf{b}$后，体积并不会发生改变。

我们可以发现，这个就正好对应着行列式的一个很重要的性质——用矩阵的一行减去另一行的倍数，行列式不变。这也是行列式是体积的一个表现。

接下来我们讨论如何从平行四边形变换成矩形，并保持体积不变。这时，我们可以想到Gram-Schmidt正交化。我们直接考虑n维情形，对${v_1,\cdots,v_n}$应用Gram-Schimidt正交化：

$$
\begin{aligned}
v_1 & =v_1 \\
v_2^{\perp} &= v_2 - c_{12} v_1 \\
v_3^{\perp} &= v_3 - c_{13} v_1-c_{23} v_2 \\
& \vdots
\end{aligned}
$$

可以发现，正好对应着上面提到的变换。因此，这一组正交基张成的平行多面体的体积与原向量张成的平行多面体的体积相等。

记$U=(v_1,v_2^\perp,\cdots,v_n^\perp)$，可以知道：

$$
UU^T=diag(||v_1||^2,\cdots,||v_n^\perp||^2)
$$

求行列式：

$$
|UU^T|=||v_1||^2\cdots ||v_n^\perp||^2
$$

由于$|UU^T|=|U||U^T|=|U|^2$，所以$|U|=||v_1||\cdots || v_n^\perp ||$，即平行多面体的体积。这个体积也等于原向量张成的平行多面体的体积，得证。

非方阵的”行列式“

根据上面的分析，我们知道了n阶方阵的行列式表示n个列向量张成的平行多面体的体积。那么如何求n维空间中m个列向量张成的平行多面体的体积呢？

n维空间中m个列向量构成了一个$n\times m$的矩阵，记为$A$。我们知道行列式表示体积，但是只有方阵才有行列式，那应该如何处理呢？

如果m个列向量线性相关，那么张成的平行多面体体积一定为0。因此，只考虑$n>m$，且m个列向量均线性无关的情况。

为了应用行列式的结论，我们可以考虑将此m维多面体放到m维空间中，那么就需要对空间进行变换。但是，要求在变换过程中，不会改变空间的几何结构，即该多面体的体积。由于正交变换不改变几何结构，因此，可以使用QR分解。

利用Gram-Schmidt正交化方法进行QR分解，可得：

$$
A=QR,其中Q\in C^{n\times m},R\in C^{m\times m}
$$

其中$Q$的每一列构成了一组标准正交基，因此$Q^TQ=I_{m\times m}$，可得：$Q^TA=R$。

$$
\begin{aligned}
V &= |detR| \\
&= \sqrt{|det(R^TR)|} \\
&= \sqrt{|det((Q^TA)^TQ^TA)|} \\
&= \sqrt{|det(A^TA)|}
\end{aligned}
$$

因此，体积为$\sqrt{|det(A^TA)|}$。从一定角度上讲，这个式子可以当成非方阵的”行列式“，因为它们的几何意义是相同的。

楔积

接下来站在一个更高的角度来看待这个行列式。对于行列式，我们知道交换两列或两行后，会改变符号。根据行列式的几何意义，行列式表示平行多面体的体积，因此，从一定程度上说，这个平行多面体应该有符号，或者说是有方向，对应着行列式交换两列后符号的变化。行列式的这个特性被称为反对称性，德国科学家Grassmann将这个特性推广到了n维空间中，方法就是使用楔积(Wedge Product)。其具有两个特性：

1. （多重线性）：$\cdots \wedge(\lambda \vec{v}+\mu \vec{u}) \wedge \cdots=\lambda(\cdots \wedge \vec{v} \wedge \ldots)+\mu(\cdots \wedge \vec{u} \wedge \ldots)$
2. （反对称性）：$\cdots \wedge \vec{v} \wedge \cdots \wedge \vec{u} \wedge \cdots=(-1) \cdots \wedge \vec{u} \wedge \cdots \wedge \vec{v} \wedge \ldots$

可以通过二维情况来理解这个式子。

$$
\begin{aligned} \mathbf{a} \wedge \mathbf{b}&=\left(a_1 \mathbf{e}_1+a_2 \mathbf{e}_2\right) \wedge\left(b_1 \mathbf{e}_1+b_2 \mathbf{e}_2\right) \\
&=a_1 b_1 \mathbf{e}_1 \wedge \mathbf{e}_1+a_1 b_2 \mathbf{e}_1 \wedge \mathbf{e}_2+a_2 b_1 \mathbf{e}_2 \wedge \mathbf{e}_1+a_2 b_2 \mathbf{e}_2 \wedge \mathbf{e}_2 \\
&= (a_1b_2-a_2b_1)\mathbf{e}_1 \wedge \mathbf{e}_2
\end{aligned}
$$

可以发现，其系数与行列式相对应，我们可以写成：

$$
|A|=\frac{\mathbf{a}\wedge \mathbf{b}}{\mathbf{e}_1 \wedge \mathbf{e}_2}
$$

也可以写成：

$$
|A|=||\mathbf{a} \wedge \mathbf{b}||
$$

因此，我们可以推测，n维空间中n个列向量的楔积，其范数就等于行列式（证明略），即对于n阶方阵$A$，有：

$$
|A|=||a_1\wedge\cdots \wedge a_n||
$$

实际上，我们知道，楔积是有方向性的，因此，楔积的几何意义就是以这些向量为边“拼成”的平行多面体，并且改变排列会影响图形的”正负“，所以可以将其称为一个具有方向和大小的向量。从这个角度，我们看下面这个式子：

$$
|A|=\frac{\mathbf{a}\wedge \mathbf{b}}{\mathbf{e}_1 \wedge \mathbf{e}_2}
$$

可以将$A$看作一个算子，作用于基向量。然后n维图形发生了变化，其变化率就是算子$A$的行列式。

因此，在线性空间$V$中选取一组基${v_1,\cdots,v_n}$，算子的行列式可以定义为：

$$
\operatorname{det} T=\left(T \overrightarrow{\mathrm{v}}_1 \wedge T \overrightarrow{\mathrm{v}}_2 \wedge \cdots \wedge T \overrightarrow{\mathrm{v}}_n\right) /\left(\overrightarrow{\mathrm{v}}_1 \wedge \overrightarrow{\mathrm{v}}_2 \wedge \cdots \wedge \overrightarrow{\mathrm{v}}_n\right)
$$

回到上面非方阵的”行列式“的那个问题，根据楔积的几何意义，我们可以很容易写出答案：

$$
V=||a_1\wedge \cdots \wedge a_m||
$$

楔积不仅适用于方阵，也适用于非方阵。这个结果的证明可以将这两种方法的结果求出来，然后比较系数即可，由于过于繁琐，就省略了。同时，还有另外一个角度可以简略的说明，因为楔积是一个有方向的量，因此，可以定义内积，如下：

$$
\vec{A} \cdot \vec{B}=\left(\vec{a}_1 \wedge \cdots \wedge \vec{a}_k\right) \cdot\left(\vec{b}_1 \wedge \cdots \wedge \vec{b}_k\right)=\left|\begin{array}{ccc}
\vec{a}_1 \cdot \vec{b}_1 & \ldots & \vec{a}_1 \cdot \vec{b}_k \\
\vdots & \ddots & \vdots \\
\vec{a}_k \cdot \vec{b}_1 & \ldots & \vec{a}_k \cdot \vec{b}_k
\end{array}\right|=\operatorname{det}\left(A^{\top} B\right)
$$

那么，$A$与自身的内积就是其平行多面体的体积的平方，即范数$|A|=\sqrt{\operatorname{det}\left(A^{\top} A\right)}$ 就是$A$的体积。

行列式的代数意义

我们知道行列式是线性的，现在我们引入重线性函数的概念。

重线性函数

令 $V^k=V \times V \times \cdots \times V$ 是 $k$ 个线性空间 $V$ 的个笛卡尔积, 则一个函数 $f: V^k \rightarrow R$ 是 $V$ 上的 $k$ 重线性函数, 是指对于它的任意一个分量, 该函数都是线性的:
$$
f\left(\cdots, a \mathbf{v}_1+b \mathbf{v}_2, \cdots\right)=a f\left(\cdots, \mathbf{v}_1, \cdots\right)+b f\left(\cdots, \mathbf{v}_2, \cdots\right)
$$

显然，对于一个n阶行列式，不论对于哪一列，都是线性的，因此，行列式是一个n重线性函数。

对称重线性函数与交代重线性函数

一个 $k$ 线性函数 $f: V^k \rightarrow R$ 是对称的, 如果对于 $k$ 阶置换群 中的所有元素 $\sigma \in S_k$, 都有
$$
f\left(\mathbf{v}_{\sigma(1)}, \cdots, \mathbf{v}_{\sigma(k)}\right)=f\left(\mathbf{v}_1, \cdots, \mathbf{v}_k\right)
$$
一个 $k$ 线性函数 $f: V^k \rightarrow R$ 是交代的, 如果对于 $k$ 阶置换群 中的所有元素 $\sigma \in S_k$, 都有
$$
f\left(\mathbf{v}_{\sigma(1)}, \cdots, \mathbf{v}_{\sigma (k) }\right)=\operatorname{sgn}\left(\sigma) f\left(\mathbf{v}_1, \cdots, \mathbf{v}_k\right)\right.
$$

其中，对于置换群，举个例子，对于(1,2,3)，其置换有(1,2,3),(2,3,1),(3,1,2),(2,1,3),(1,3,2),(3,2,1)，这就构成了一个置换群。对于交代中的$sgn(\sigma)$，这表示置换的奇偶性，其值与逆序数的奇偶是一致的。因此，我们可以把交代看作是反对称在高维上的推广。

因此，我们可以知道行列式是交代重线性函数。那么交代这种性质有没有一种代数表达呢？答案是有的，这就对应着一个交代张量。这就是行列式的代数意义，即对应着交代张量。因此，从这里也能看出，张量是站在一个更高的角度上看待数学问题，行列式只是张量的一个应用。

$$
\operatorname{det}(\mathbf{A})=\operatorname{det}\left(\left[\begin{array}{llll}
\mathbf{a}_1 & \mathbf{a}_2 & \cdots & \mathbf{a}_n
\end{array}\right]\right)=\boldsymbol{A} \times_1 \mathbf{a}_1 \times_2 \mathbf{a}_2 \cdots \times_n \mathbf{a}_n
$$

其中$\boldsymbol{A}$不是等式左边的矩阵，而是交代张量。$\times_n$表示张量乘积。关于这个，由于我也没学过张量，只能做一个简单的解释。对于二维情况，如下：

$$
\operatorname{det}(\mathbf{A})=\left[\begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array}\right] \times_1 \mathbf{a}_1 \times_2 \mathbf{a}_2=\left[\begin{array}{ll}
a_{11} & a_{21}
\end{array}\right]\left[\begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array}\right]\left[\begin{array}{l}
a_{12} \\
a_{22}
\end{array}\right]
$$

这个就表示张量从第一个方向乘$a_1$，从第二个方向乘$a_2$，对于矩阵来说，只有左乘和右乘，因此，只有两个方向，上式就是$a_1$右乘，$a_2$左乘。对于三维情况，交代张量并不是一个简单的矩阵，而是一个三层的结构，如下：

$$
\boldsymbol{A}(:,:, 1)=\left[\begin{array}{ccc}
0 & 0 & 0 \\
0 & 0 & 1 \\
0 & -1 & 0
\end{array}\right], \boldsymbol{A}(:,:, 2)=\left[\begin{array}{ccc}
0 & 0 & -1 \\
0 & 0 & 0 \\
1 & 0 & 0
\end{array}\right], \boldsymbol{A}(:,:, 3)=\left[\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]
$$

三维情况，写成：

$$\operatorname{det}(\mathbf{A})=\boldsymbol{A} \times_1 \mathbf{a}_1 \times_2 \mathbf{a}_2 \times_3 \mathbf{a}_3$$

表示张量A分别从三个方向乘三个列向量。由于矩阵只有两个方向，因此没办法像二维情况写成矩阵相乘。这就引入了n模积，来求张量乘法。

$n$ 模积指的是张 量与矩阵的乘积，给定张量 $\mathcal{A} \in R^{I_1 \times I_2 \times \ldots \times I_N}$ ，矩阵 $U \in R^{J_n \times I_n}$ ，则张量 $\mathcal{A}$ 和矩阵 $U$ 的 $\mathrm{n}$ 模积表示为 $\mathcal{A}_{\times n} U$ ，是一个 $I_1 \times I_2 \times \ldots \times I_{n-1} J_n I_{n+1} \times \ldots \times I_N$ 的张量。并且张量 $\mathcal{A}_{\times n} U$ 中的元素具有如下计算公式
$$
\left(\mathcal{A}_{\times n} U\right)_{i_1 i_2 \ldots i_{n-1} j_n i_{n+1} \ldots i_N}=\sum_{i_n=1}^{I_n} a_{i_1 i_2 \ldots i_{n-1} i_n i_{n+1} \ldots i_N} u_{j_n i_n}
$$

具体就不展开了（因为我也不会了）。

行列式的应用

考虑如下问题：

如何选择合适的R，G，B三波段，使得假色彩合成图具有更多的信息量？假如我们有50个波段的数据，选择其中的三个波段。

从问题中可以看出，希望找出三个最不相似的波段，或者说是相差最远的波段。因此，可以考虑三个波段构成的图形，当此图形体积最大时，说明此三个波段相差最远，因此，我们可以采用体积标准，即$det(XX^T)$，转为优化问题。

行列式优化问题的求解

那么如何求解这个优化问题呢？首先我们能够想到穷举法。

对所有的情况均进行求行列式，找出最大值即可。但是显然这有着很大的计算量，尤其是当我们需要选择更多的波段时，计算量将会很大很大。

一个较好的方法是后向法。即对这50个波段，删除其中的一个波段，求行列式，找到值最大的情况，说明剩下的49个波段最不相似。然后继续往下找，我们可以依次得到最不相似的48、...、2的波段。相比于第一个算法，就少算了许多重复的情况。但是这还是要算很多种情况，接下来我们从理论上对算法进行改进。

利用梯度信息，求导得：

$$
\begin{aligned}
\mathbf{D}&=\frac{\partial \operatorname{det}\left(\mathbf{X X}^T\right)}{\partial \mathbf{X}} \\
& =2 \operatorname{det}\left(\mathbf{X} \mathbf{X}^T\right)\left(\mathbf{X} \mathbf{X}^T\right)^{-1} \mathbf{X}
\end{aligned}
$$

注：这个利用了矩阵的微积分，感兴趣的可以去网上查找资料。

首先，我们观察到，$DX^T=2det(XX^T)I$，这表明了对于X中的任一行A，D中在A以外的所有行与A均正交，换句话说，如果对于X，我们只能移动A，那么A沿着其余向量对应的平行多面体的垂直方向移动，才能使体积变化速度最大。

并且，我们将这个50维的平行多面体，看成49维多面体乘以高h，再乘一个系数（系数不重要），我们可以得到：

$$
\begin{aligned}
& V_m=\frac{1}{(m-1) !} V_{m-1} h \\
& d V_m=\frac{1}{(m-1) !}\left(\left(d V_{m-1}\right) h+V_{m-1} d h\right) \\
& d V_m=\frac{1}{(m-1) !} V_{m-1} d h \\
& V_{m-1}=(m-1) \frac{d V_m}{d h}
\end{aligned}
$$

在上式中，可以发现，49维多面体的体积，与$XX^T$相比于高h的梯度成正比。根据上述分析，这个相对高的梯度，等价于$||\frac{\partial \operatorname{det}\left(\mathbf{X X}^T\right)}{\partial \mathbf{A}}||$。而这正好是D中的与A相对应的行向量的范数。这得到了一个十分重要的结论，也就是$D$的每一行向量的范数也是有意义的，第$i$行的范数与$X$去掉第$i$行后围成的多面体的体积成正比，这正好对应着上面的后向法。

那么，我们只需要求$D$，然后找出范数最大的那一行，就可以很容易知道删除哪一个波段，由此可见，只需要计算一次，就可以删除一个，而不是后向法中的计算50次。

这个方法还可以进一步进行改进。我们知道$D$的每一行的范数是有意义的，因此，我们可以通过计算：

$$
\begin{aligned}
\mathbf{D D}^{\mathrm{T}}&=2 \operatorname{det}\left(\mathbf{X X}^{\mathrm{T}}\right)\left(\mathbf{X X}^{\mathrm{T}}\right)^{-1} \mathbf{X}\left(2 \operatorname{det}\left(\mathbf{X X}^{\mathrm{T}}\right)\left(\mathbf{X X}^{\mathrm{T}}\right)^{-1} \mathbf{X}\right)^{\mathrm{T}} \\
& =4 \operatorname{det}\left(\mathbf{X X}^{\mathrm{T}}\right)^2\left(\mathbf{X X}^{\mathrm{T}}\right)^{-1} \mathbf{X} \mathbf{X}^{\mathrm{T}}\left(\mathbf{X X}^{\mathrm{T}}\right)^{-1}=c\left(\mathbf{X X}^{\mathrm{T}}\right)^{-1}
\end{aligned}
$$

我们知道，$DD^T$的对角元素就对应着每一行的范数。这也就是说，$\left(\mathbf{X X}^{\mathrm{T}}\right)^{-1}$的对角线元素就反映了$D$的每一行的范数。好了，到这里，我们甚至都不需要求$D$了，只需要求$\left(\mathbf{X X}^{\mathrm{T}}\right)^{-1}$就可以了。

但是这样，删除一次，我们都需要重新计算一次，那么还有没有办法进行改进呢？当然有。如果我们知道了$\left(\mathbf{X X}^{\mathrm{T}}\right)^{-1}$，然后当$X$删除了一行之后，能够直接得到更新后的$\left(\mathbf{X' X'}^{\mathrm{T}}\right)^{-1}$呢？

可以利用分块矩阵的逆的求法。

已知：

$$
\left[\begin{array}{ll}
\mathbf{A} & \mathbf{u} \\
\mathbf{u}^T & d
\end{array}\right]^{-1}=\left[\begin{array}{cc}
\mathbf{A}^{-1}+\mathbf{A}^{-1} \mathbf{u}\left(d-\mathbf{u}^T \mathbf{A}^{-1} \mathbf{u}\right)^{-1} \mathbf{u}^T \mathbf{A}^{-1} & -\mathbf{A}^{-1} \mathbf{u}\left(d-\mathbf{u}^T \mathbf{A}^{-1} \mathbf{u}\right)^{-1} \\
-\left(d-\mathbf{u}^T \mathbf{A}^{-1} \mathbf{u}\right)^{-1} \mathbf{u}^T \mathbf{A}^{-1} & \left(d-\mathbf{u}^T \mathbf{A}^{-1} \mathbf{u}\right)^{-1}
\end{array}\right]
$$

其中，$u$为向量。

假设 $\mathbf{C}=\left[\begin{array}{cc}\mathbf{A} & \mathbf{u} \\ \mathbf{u}^T & d\end{array}\right]$, 且 $\mathbf{C}^{-1}=\left[\begin{array}{cc}\mathbf{A} & \mathbf{u} \\ \mathbf{u}^T & d\end{array}\right]^{-1} \stackrel{\text { 记 }}{=}\left[\begin{array}{ll}\hat{\mathbf{C}} & \mathbf{c} \\ \mathbf{c}^T & c\end{array}\right]$

则有 $\mathbf{A}^{-1}=\hat{\mathbf{C}}-\frac{\mathbf{c c}^T}{c}$

有了这个理论，最开始时，$XX^T$为50阶矩阵，我们对其求逆，得到了一个结果，就是上式中的$C$。然后根据对角线元素，找出最大值，知道了要删除的行。将要删除的行向量作为上式中的$u$，更新后的$X'X'^T$就是上式中的$A$。根据上式中的公式，可以直接得到$\left(\mathbf{X' X'}^{\mathrm{T}}\right)^{-1}$。因此，就不用再重新算$XX^T$了，节省了计算量。