行列式

空间在经历了线性变换后，线性变换在空间中表现为对空间进行了拉伸或者收缩，而我们应该如何衡量这种改变呢？

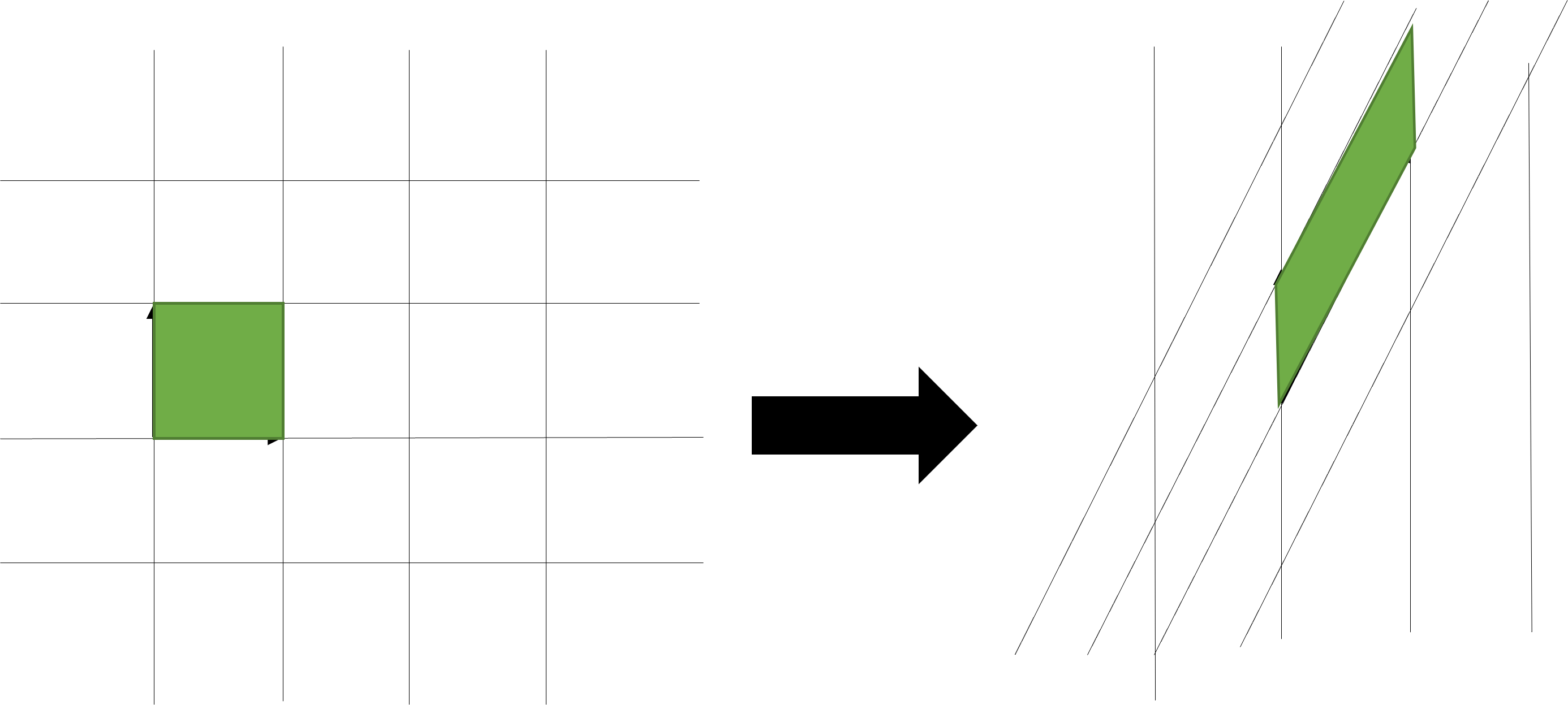
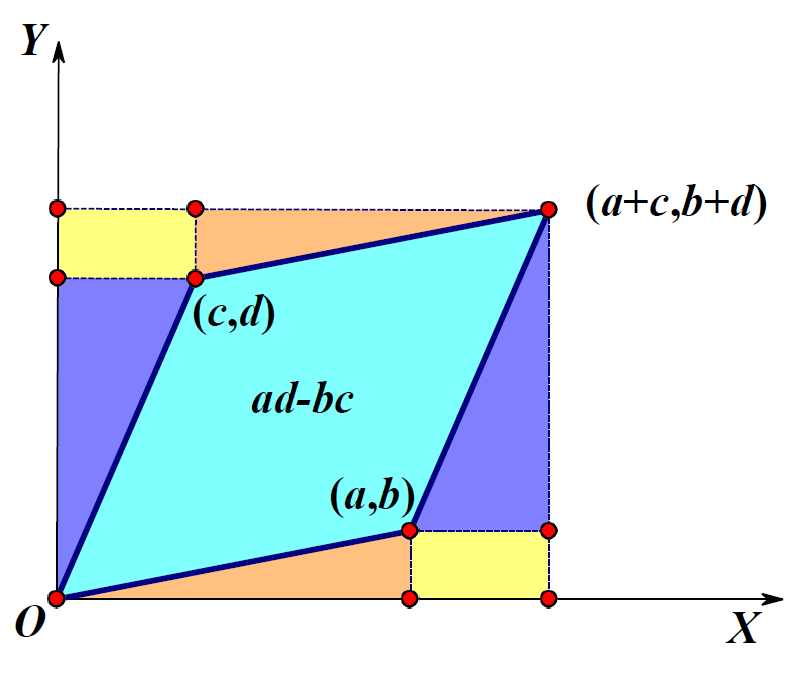
一个空间是由基向量为基础构成的，因此我们可以用基向量组成的区域来衡量这种改变。在二维情形下，这个区域就是两个基向量组成的平行四边形的面积，如下图所示。线性变换对空间进行了拉伸，这个面积也发生的一定的变化。衡量这个面积变化量的量就是行列式(Determinant)。

考虑一种特殊情况，当变换后，两组基向量变成线性相关了，比如$\begin{bmatrix}0 & 0 \\ 1 & 3 \end{bmatrix}$，在空间中，这个表现为两组基向量组成的区域面积为0，所以面积变化了$0/1=0$倍，说明这个矩阵的行列式为0，此时对应着空间的维度发生了降低，即出现了降维。因此，可以得到一个对应关系：
$$
线性相关 \Leftrightarrow Det(M)=0
$$
使用行列式的含义来考虑对角矩阵的值。例如对对角矩阵$\begin{bmatrix}a & 0 \\ 0 & b \end{bmatrix}$，它表示第一个基向量变为了$\vec{i}$的a倍，第二个基向量变为了$\vec{j}$的b倍，然后我们可以得到它们组成的区域面积变为了原来的ab倍，即这个行列式的值为ab，是不是很直观呢？

再考虑一个行列式的性质：Det(M₁M₂)=Det(M₁)Det(M₂)。在教材中，这个性质的证明是十分繁琐的。在这里，我们就使用上面行列式的含义来解释，可以发现很容易解释这个性质，而不需要繁琐的理论计算。M₁M₂表示两个线性变换的组合，先进行M₂变换，面积变为了最初的Det(M₂)倍，然后进行M₁变换，面积变为了M₂变换后的Det(M₁)倍，因此，面积为最初的Det(M₁)Det(M₂)倍。而如果同时把M₁M₂的结果作为一次线性变换，那么可以得到面积为最初的Det(M₁M₂)倍，故这个性质是成立的。是不是很简单？

线性方程组，逆

在上面的介绍中，矩阵是扮演着变换空间的能力。接下来谈一下矩阵在线性方程组(Linear System of Equations)中的应用，这也是线性代数中的一个重点。

线性方程组通常表示为$\mathbf{\mathit{A} } x=b$，其中A为系数矩阵，x为未知量，b为值。其中，x和b均为向量。我们可以与前面的知识联系起来，看看在空间中，这个等式有什么含义。首先，x和b是两个向量，A是矩阵，存储着一个线性变换的信息，那么这个式子的含义就很明显了，对x进行A对应的线性变换之后，与b重合，而我们就是找这个能够与b重合的x。这就与前面的知识联系起来了，然后线性方程组也就没什么特殊的了。

将这个与前面的知识结合起来来理解。根据前面的知识，我们也可以知道，当det(A)不等于0时，线性变换前后的向量是一一对应的，那么这个方程组就存在唯一解。而当det(A)等于0，那么发生了降维。这时，将不一定有解。为什么呢？例如对于二维情况，如果降至一维，即一条直线，那么只有当b恰好在这条直线上时，才存在解，此时有无穷多个解。为什么有无穷多个解呢？在下面介绍零空间就会得到答案，简单来说，就是降维时，存在多对一的映射，比如2D到1D中，直线到点的映射，故存在无穷多个向量能够映射上b上，因此存在无穷多个x。而如果b不在这个直线上，且b不为0，那么将不存在解，这个很好理解，因为没有向量经过线性变换后得到b。

那么如何求解呢？我们可以将这个过程反过来看，对x施加A线性变换得到b，那么对b施加一个线性变换后是不是也能得到x呢？答案是肯定的（当然这里指的不是特殊情况，比如行列式为0）。而这个相反的线性变换就是A的逆(Inverse)，表示为A^-1。

考虑A^-1A，表示先施加A对应的线性变换，然后施加A^-1对应的线性变换，相当于将这个空间变换来再变换回去，相当于并没有变换，因此可以得到A^-1A=E.

根据上面的分析，当det(A)不为0时，A^-1是肯定存在的。而当det(A)=0，那么维度降低，逆将不存在。这是为什么呢？

我们可以根据函数来理解这个。一个函数只能够根据一个输入得到一个输出，而不能根据一个输入得到多个输出。这对于矩阵也是一样的，降了之后，没办法升回去，故不存在逆。（注：我们现在讨论的都是方阵，如果不是方阵，确实能够升维，但不是现在讨论的范畴）

秩

从前面的分析中可以看出，在应用线性变换时，会存在降维的情况。对于二维情况，可能会降至一维，甚至0维，而对于三维情况，可能会降至二维，也可能会降至一维，存在很多种情况。那么我们应该如何衡量呢？

衡量输出空间维度的量就是秩(Rank)，也就是线性变换后的维度。

考虑原点(Origin)，当维度不变时，输出空间的原点仅与输入空间中的原点对应，但发生降维后，如果二维降至一维，则输出空间中的原点来源于输入中的一条线，如果三维降至二维，那么输出空间中的原点来源于输入空间中的一个平面。而这三种情况中的点、线或者平面，称为零空间(null space)或者核(kernel)，定义为经过变换后落在原点的向量的集合(the set of vectors that lands on the origin)。

不只是原点，当二维降至一维时，输出空间的每一个点都来源于输入的一条直线，这也就是为什么线性方程组中在一些特殊情况下会有无穷多个解。再考虑一个特殊情况，如果Det(A)=0，当解为零向量时，那么相当于求解经过线性变换落到原点的向量，此时将肯定存在无穷多个解，且这个解为零空间。因为无论怎么线性变换，零点的位置是不变的，当Det(A)=0时，说明发生了降维，此时零空间肯定会是过原点的直线或平面或更高维的东西。

最后简单介绍以下不是方阵的情况。前面介绍的情况都是维度不变或者降低，但如果我们想将2维变成3维呢？这种变换对应的就是非方阵，之前介绍的都是方阵。其矩阵中的基向量需要与输出维度对应，例如由2D到3D，变换矩阵需要时3*2的，即每一列是三维的。之所以不重点提这个，因为这个并不影响我们去理解线性代数的本质，而且方阵也是最常用的。